
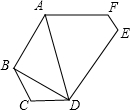
 如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,BC∥EF.
如图,六边形ABCDEF中,∠A=∠D,∠B=∠E,BC∥EF.分析 (1)连接CF,AC,根据平行线性质得出∠EFC=∠FCB,根据∠A=∠D,∠B=∠E,求出∠AFC=∠DCF,根据平行线的判定得出即可;
(2)根据平行线的性质和三角形的内角和定理得出∠FAC+∠ACD=180°,∠B+∠BAC+∠CB=180°,相加即可得出答案.
解答 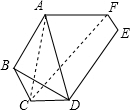 (1)证明:连接CF,AC,
(1)证明:连接CF,AC,
∵BC∥EF,
∴∠EFC=∠FCB,
∵∠A=∠D,∠B=∠E,
∴∠AFC=∠DCF,
∴AF∥CD;
(2)解:∵AF∥CD,
∴∠FAC+∠ACD=180°,
∵∠B+∠BAC+∠CB=180°,
∴∠FAC+∠ACD+∠B+∠BAC+∠ACB=360°,
即∠FAB+∠B+∠BCD=360°.
点评 本题考查了平行线的性质和判定,三角形内角和定理的应用,能灵活运用性质进行推理是解此题的关键,注意:平行线的性质有①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AF∥CD,AB⊥BC,∠A=122°.
如图,AF∥CD,AB⊥BC,∠A=122°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(公斤/辆) | 600 | 800 | 900 |
| 汽车运费(元/辆) | 500 | 600 | 700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
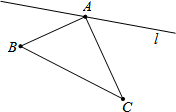 如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com