
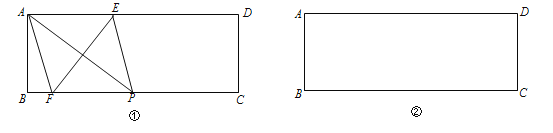
【题目】如图,在矩形ABCD中,AB=1,BC=3.
(1)在图①中,P是BC上一点,EF垂直平分AP,分别交AD、BC边于点E、F,求证:四边形AFPE是菱形;
(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD的边上,并直接标出菱形的边长.(保留作图痕迹,不写作法)
【答案】(1)见解析;(2)见解析
【解析】
(1)根据矩形的性质和EF垂直平分AP推出AF=PF=AE=PE即可判断;
(2)以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,此时的菱形即为矩形ABCD内面积最大的菱形.
(1)证明:如图①
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠2,
∵EF垂直平分AP,
∴AF=PF,AE=PE,
∴∠2=∠3,
∴∠1=∠3,
∴AE=AF,
∴AF=PF=AE=PE,
∴四边形AFPE是菱形;

(2)如图②,以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,连接各个点,所得的菱形即为矩形ABCD内面积最大的菱形;
此时设菱形边长为x,
则可得12+(3-x)2=x2,
解得x=![]() ,
,
所以菱形的边长为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华是花店的一名花艺师,她每天都要为花店制作普通花束和精致花束,她每月工作20天,每天工作8小时,她的工资由基本工资和提成工资两部分构成,每月的基本工资为l800元,另每制作一束普通花束可提2元,每制作一束精致花束可提5元.她制作两种花束的数量与所用时间的关系见下表:
制作普通花束(束) | 制作精致花束(束) | 所用时间(分钟) |
10 | 25 | 600 |
15 | 30 | 750 |
请根据以上信息,解答下列问题:
(1)小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟?
(2)2019年11月花店老板要求小华本月制作普通花束的总时间![]() 不少于3000分钟且不超过5000分钟,则小华该月收入
不少于3000分钟且不超过5000分钟,则小华该月收入![]() 最多是多少元?此时小华本月制作普通花束和制作精致花束分别是多少束?
最多是多少元?此时小华本月制作普通花束和制作精致花束分别是多少束?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄![]() ,河边原有两个取水点
,河边原有两个取水点![]() ,其中
,其中![]() ,由于某种原因,由
,由于某种原因,由![]() 到
到![]() 的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点
的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点![]() 在同一条直线上),并新修一条路
在同一条直线上),并新修一条路![]() ,测得
,测得![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
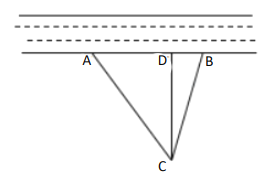
(1)问![]() 是否为从村庄
是否为从村庄![]() 到河边最近的路?请通过计算加以说明:
到河边最近的路?请通过计算加以说明:
(2)求原来的路线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E,F,连接EF.
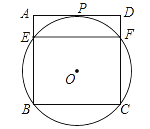
(1)求证:PF平分∠BFD;
(2)若tan∠FBC= ![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y最小= ;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+![]() (x>0)的最小值,解决问题(2)
(x>0)的最小值,解决问题(2)
【解决问题】
(2)直接写出“问题情境”中问题的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条(
条(![]() ).
).
(1)客户分别按方案①、方案②购买,各需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com