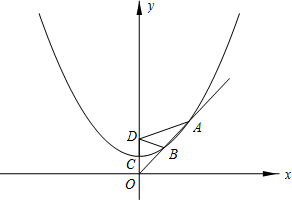
解:(1)设抛物线的解析式为y=kx
2+a,
∵经过点(2a,2a),
4a
2k+a=2a,
∴k=

,
则抛物线的解析式为:y=

x
2+a;
(2)连接PD,设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,
在Rt△GDP中,由勾股定理得:PD
2=DG
2+PG
2=(y-2a)
2+x
2=y
2-4ay+4a
2+x
2,

∵y=

x
2+a,
∴x
2=4a×(y-a)=4ay-4a
2,
∴PD
2=y
2-4ay+4a
2+4ay-4a
2=y
2=PH
2,
∴PD=PH,
(3)过B作BE⊥x,AF⊥x,
由(2)的结论:BE=DB,AF=DA,
∵DA=2DB,
∴AF=2BE,
∴AO=2OB,
∴B是OA的中点,
∵C是OD的中点,
连接BC,∴BC=

=
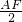
=BE=DB,
过B作BR⊥y,
∵BR⊥CD,
∴CR=DR,OR=a+

=

,
∴

=

x
2+a,
∴x
2=2a
2,
∵x>0,
∴x=

a,
∴B(

a,

),AO=2OB,
∴S
△OBD=S
△ABD=4

,
∴

×2a×

a=4

,
∴a2=4,
∵a>0,
∴a=2,
分析:(1)根据抛物线的图象假设出解析式为y=kx
2+a,将经过点(2a,2a),代入求出即可;
(2)根据勾股定理得出PD
2=DG
2+PG
2,进而求出PD=PH;
(3)利用(2)中结论得出BE=DB,AF=DA,即可得出B是OA的中点,进而得出S
△OBD=S
△ABD=4

,即可得出a的值.
点评:此题主要考查了二次函数的综合应用以及勾股定理的应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.

 .求a的值.
.求a的值.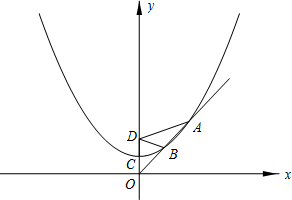
 ,
, x2+a;
x2+a;
 x2+a,
x2+a, =
=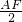 =BE=DB,
=BE=DB, =
= ,
, =
= x2+a,
x2+a, a,
a, a,
a, ),AO=2OB,
),AO=2OB, ,
, ×2a×
×2a× a=4
a=4 ,
, ,即可得出a的值.
,即可得出a的值.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案