
【题目】如图,在平面直角坐标系![]() 中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
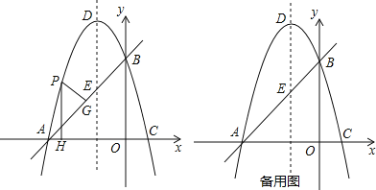
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线![]() 上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
【答案】(1)y=-x2-2x+3;(2)![]() .(3)M1(-2,3),M2(
.(3)M1(-2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).
【解析】
试题分析:(1)将已知点的坐标代入二次函数的解析式利用待定系数法确定二次函数的解析式即可;
(2)首先根据△PFG是等腰直角三角形,设P(m,-m2-2m+3)得到F(m,m+3),进而得到PF=-m2-2m+3-m-3=-m2-3m,从而得到△PFG周长为:-m2-3m+![]() (-m2-3m),配方后即可确定其最大值;
(-m2-3m),配方后即可确定其最大值;
(3)当DM1∥AB,M3M2∥AB,且与AB距离相等时,根据同底等高可以确定△ABM与△ABD的面积相等,分别求得直线DM1解析式为:y=x+5和直线M3M2解析式为:y=x+1,联立之后求得交点坐标即可.
试题解析:(1)∵直线AB:y=x+3与坐标轴交于A(-3,0)、B(0,3),
代入抛物线解析式y=-x2+bx+c中,得:
![]() ,
,
∴![]()
∴抛物线解析式为:y=-x2-2x+3;
(2)∵由题意可知△PFG是等腰直角三角形,
设P(m,-m2-2m+3),
∴F(m,m+3),
∴PF=-m2-2m+3-m-3=-m2-3m,
△PFG周长为:-m2-3m+![]() (-m2-3m),
(-m2-3m),
=-(![]() +1)(m+
+1)(m+![]() )2+
)2+![]() ,
,
∴△PFG周长的最大值为:![]() .
.
(3)点M有三个位置,如图所示的M1、M2、M3,都能使△ABM的面积等于△ABD的面积.
此时DM1∥AB,M3M2∥AB,且与AB距离相等,
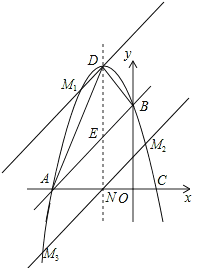
∵D(-1,4),
∴E(-1,2)、则N(-1,0)
∵y=x+3中,k=1,
∴直线DM1解析式为:y=x+5,
直线M3M2解析式为:y=x+1,
∴x+5=-x2-2x+3或x+1=-x2-2x+3,
∴x1=-1,x2=-2,x3=![]() ,x4=
,x4=![]() ,
,
∴M1(-2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家游泳中心——“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260000平方米,将260000用科学记数法表示应为( )
A. 2.6×105 B. 26×104 C. 0.26×102 D. 2.6×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是三角形的三边长,如果满足(a﹣5)2+|b﹣12|+c2﹣26c+169=0,则三角形的形状是( )
A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,关于x 的一元二次方程是( )
A. x—2x—3=0 B. x- 2y- 1=0
C. x-x(x+3)=0 D. ax+bx +c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
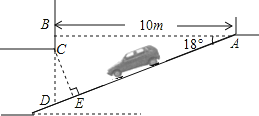
【题目】为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() .按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算
.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算![]() 的长,并标明限制高度.(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
的长,并标明限制高度.(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com