
【题目】问题探究:
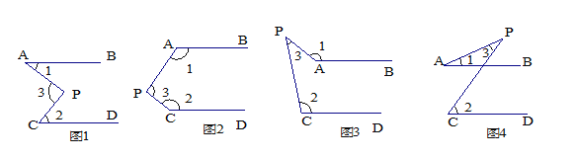
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
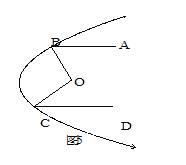
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
【答案】(1) 图1:∠1+∠2=∠3; 图2:∠1+∠2+∠3=180o; 图3:∠1=∠2+∠3; 图4:∠1+∠3=∠2;(2)见解析;(3)101o
【解析】
(1) 图1:首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
图2:首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
图3:由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
图4:由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
(2)选图1,过过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)利用图1结论进行求解.
(1)图1:∠1+∠2=∠3;
图2:∠1+∠2+∠3=180o;
图3:∠1=∠2+∠3;
图4:∠1+∠3=∠2;
(2)选择图1,
如图所示:过点P作EP//AB,

∵AB//CD,EP//AB,
∴AB//EP//CD,
∴∠1=∠APE,∠2=∠EPC,
又∵∠3=∠APE+∠EPC,
∴∠1+∠2=∠3;
(3)由图1可得:∠BOC=∠ABO+∠DCO,
又∵∠ABO=57°,∠DCO=44°,
∴∠BOC=57°+44°=101o.


科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识重现)我们知道,在axN中,已知底数a,指数x,求幂N的运算叫做乘方运算.例如23=8:已知幂N,指数x,求底数a的运算叫做开方运算,例如![]() =2.
=2.
(学习新知)
现定义:如果ax=N(a0且a1),即a的x次方等于N(a0且a1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN.其中a叫做对数的底数,N叫做真数,x叫做以a为底N的对数,例如log28=3,零没有对数;在实数范围内,负数没有对数.
(应用新知)
(1)选择题:在式子log5125中,真数是_______.
(2)①计算以下各对数的值:log39=_______;log327=_______.
②根据①中计算结果,请你直接写出logaM,logaN,loga(MN)之间的关系,(其中a0且a1,M0,N0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D在边AC上,且BD=DA=BC.
(1)如图1,填空:∠A=_______.
(2)如图2,若M为线段AC上的点,过M作直线MH⊥BD于H,分别交直线AB、BC于点N、E.
①求证:△BNE是等腰三角形;
②试写出线段AN、CE、CD之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(![]() ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com