
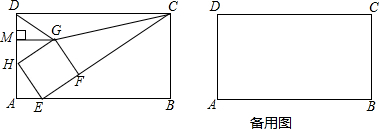
分析 (1)如图1中,只要证明△HAE≌△GMH即可解决问题;
(2)分两种情形讨论①如图2中,当0<x<8-2$\sqrt{7}$时,点G落在矩形ABCD之内,②如图3中,当8-2$\sqrt{7}$<x≤10时,点G落在矩形ABCD之外,分别求解即可解决问题;
解答 解:(1)如图1中,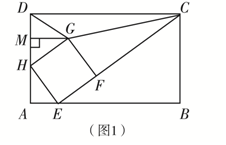
∵四边形是矩形,GM⊥AD于点,
∴∠A=∠GMH=90°,
∵四边形EFGH是正方形,
∴EH=GH,∠EHG=90°,
∴∠HGM=90°-∠GHM,∠EHA=90°-∠GHM,
∴∠HGM=∠EHA,
∴△HAE≌△GMH,
∴AH=GM.
(2)如图2中,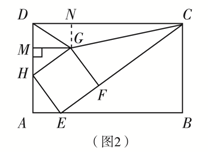
由△EAH∽△CEB,可得$\frac{AH}{BE}$=$\frac{AE}{BC}$,
∴$\frac{AH}{10-x}$=$\frac{x}{6}$,
∴AH=$\frac{x(10-x)}{6}$,
由△EAH≌△HMG,可得HM=AE=x,
当点G落在边CD上时,$\frac{x(10-x)}{6}$+x=6
解得:x=8-2$\sqrt{7}$或8+2$\sqrt{7}$(舍弃),
①当0<x<8-2$\sqrt{7}$时,点G落在矩形ABCD之内,
如图2中,作GN⊥CD于N.
∴GN=DM=6-AH-MH=6-$\frac{x(10-x)}{6}$-x,
即GN=$\frac{1}{6}$(x2-16x+36),
∴S=$\frac{1}{2}$•CD•GN=$\frac{5}{6}$x2-$\frac{40}{3}$x+30.
②当8-2$\sqrt{7}$<x≤10时,点G落在矩形ABCD之外,
如图3中,作GN⊥CD于N.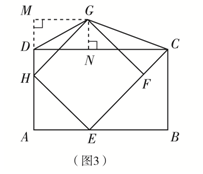
∵GN=DM=AH+HM-AD=$\frac{x(10-x)}{6}$+x-6=$\frac{1}{6}$(-x2+16x-36),
∴S=$\frac{1}{2}$•CD•GN=-$\frac{5}{6}$x2+$\frac{40}{3}$x-30.
点评 本题考查四边形综合题、矩形的性质、全等三角形的判定和性质、三角形的面积等知识,解题的关键是学会添加常用辅助线,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ACB=90°,AC=BC,点D在BC边上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q.给出以下结论:
如图,∠ACB=90°,AC=BC,点D在BC边上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q.给出以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
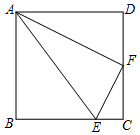 如图,正方形ABCD中,F是CD边的中点,E是BC边上一点,且AF平分∠DAE.
如图,正方形ABCD中,F是CD边的中点,E是BC边上一点,且AF平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{ax>1}\\{bx>1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{ax<2}\\{bx<2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{ax>3}\\{bx<3}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{ax<4}\\{bx>4}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com