
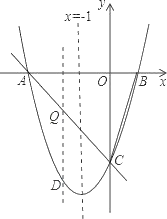
【题目】如图:对称轴x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(﹣3,0),且点(2,5)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式.
(2)点C为抛物线与y轴的交点.
①点P在抛物线上,且S△POC=4S△BOC,求点P点坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
【答案】(1)抛物线的解析式为:y=x2+2x﹣3;
(2)①点P的坐标为(4,21)或(﹣4,5);
②当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.
【解析】试题分析:(1)因为抛物线的对称轴为x=-1,A点坐标为(-3,0)与(2,5)在抛物线上,代入抛物线的解析式,即可解答;(2)①先由二次函数的解析式为y=x2+2x-3,得到C点坐标,然后设P点坐标为(x,x2+2x-3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;②先运用待定系数法求出直线AC的解析式为y=-x-3,再设Q点坐标为(x,-x-3),则D点坐标为(x,x2+2x-3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
试题解析:(1)因为抛物线的对称轴为x=﹣1,A点坐标为(﹣3,0)与(2,5)在抛物线上,则:
 ,
,
解得: 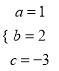 .
.
所以抛物线的解析式为:y=x2+2x﹣3.
(2)①二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴![]() ×3×|x|=4×
×3×|x|=4×![]() ×3×1,
×3×1,
∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
②设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,﹣3)代入,
得![]() ,
,
解得: ![]() .
.
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)统计图共统计了 天的空气质量情况;
(2)请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是 ;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:下列说法中,错误的是( )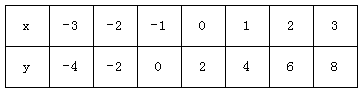
A.方程ax+b=0的解是x=-1
B.不等式ax+b>0的解集是x>-1
C.y=ax+b的函数值随自变量的增大而增大
D.y=ax+b的函数值随自变量的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形OABC,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0),当点P第2016次碰到长方形的边时,点P2016的坐标是 . 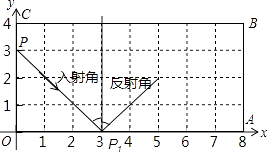
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com