
知识迁移
当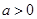 且
且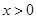 时,因为
时,因为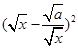 ≥
≥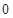 ,所以
,所以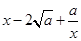 ≥
≥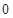 ,从而
,从而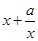 ≥
≥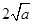 (当
(当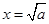 时取等号).
时取等号).
记函数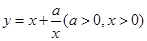 ,由上述结论可知:当
,由上述结论可知:当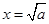 时,该函数有最小值为
时,该函数有最小值为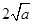
直接应用
已知函数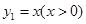 与函数
与函数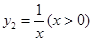 , 则当
, 则当 ____时,
____时,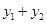 取得最小值为___.
取得最小值为___.
变形应用
已知函数 与函数
与函数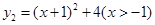 ,求
,求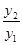 的最小值,并指出取得
的最小值,并指出取得
该最小值时相应的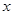 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共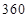 元;二是燃油费,每千
元;二是燃油费,每千
米为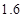 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为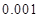 .设该汽车一次运输的路
.设该汽车一次运输的路
程为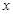 千米,求当
千米,求当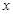 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
科目:初中数学 来源: 题型:
| x |
| ||
|
| a |
| a |
| x |
| a |
| x |
| a |
| a |
| a |
| x |
| a |
| a |
| 1 |
| x |
| y2 |
| y1 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏盐城卷)数学(带解析) 题型:解答题
知识迁移
当 且
且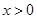 时,因为
时,因为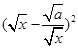 ≥
≥ ,所以
,所以 ≥
≥ ,从而
,从而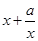 ≥
≥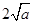 (当
(当 时取等号).
时取等号).
记函数 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为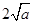
直接应用
已知函数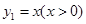 与函数
与函数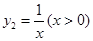 , 则当
, 则当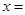 ____时,
____时,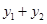 取得最小值为___.
取得最小值为___.
变形应用
已知函数 与函数
与函数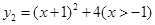 ,求
,求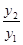 的最小值,并指出取得
的最小值,并指出取得
该最小值时相应的 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共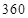 元;二是燃油费,每千
元;二是燃油费,每千
米为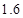 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路
.设该汽车一次运输的路
程为 千米,求当
千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源:江苏中考真题 题型:解答题
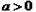 且
且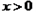 时,因为
时,因为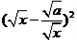 ≥
≥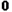 ,所以
,所以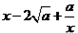 ≥
≥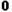 ,从而
,从而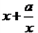 ≥
≥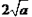 (当
(当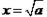 时取等号).
时取等号).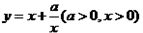 ,由上述结论可知:当
,由上述结论可知:当 时,该函数有最小值为
时,该函数有最小值为
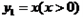 与函数
与函数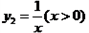 , 则当
, 则当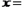 ( )时,
( )时,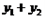 取得最小值为( )
取得最小值为( )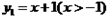 与函数
与函数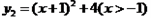 ,求
,求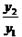 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的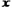 的值
的值 元;二是燃油费,每千米为
元;二是燃油费,每千米为 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为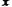 千米,求当
千米,求当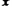 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?查看答案和解析>>
科目:初中数学 来源: 题型:
知识迁移
当![]() 且
且![]() 时,因为
时,因为![]() ≥
≥![]() ,所以
,所以![]() ≥
≥![]() ,
,
从而![]() ≥
≥![]() (当
(当![]() 时取等号).
时取等号).
记函数![]() ,由上述结论可知:当
,由上述结论可知:当![]() 时,该函数有最小值为
时,该函数有最小值为![]() .
.
直接应用
已知函数![]() 与函数
与函数![]() , 则当
, 则当![]() _________时,
_________时,![]() 取得最小值为_________.
取得最小值为_________.
变形应用
已知函数![]() 与函数
与函数![]() ,求
,求![]() 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的![]() 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共![]() 元;二是燃油费,每千米为
元;二是燃油费,每千米为![]() 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为![]() .设该汽车一次运输的路程为
.设该汽车一次运输的路程为![]() 千米,求当
千米,求当![]() 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com