
 (2010•铁岭)如图,已知矩形ABCD内接于⊙O,BD为⊙O直径,将△BCD沿BD所在的直线翻折后,得到点C的对应点N仍在⊙O上,BN交AD与点M.若∠AMB=60°,⊙O的半径是3cm.
(2010•铁岭)如图,已知矩形ABCD内接于⊙O,BD为⊙O直径,将△BCD沿BD所在的直线翻折后,得到点C的对应点N仍在⊙O上,BN交AD与点M.若∠AMB=60°,⊙O的半径是3cm. 解:(1)过点O作OG⊥ND于点G
解:(1)过点O作OG⊥ND于点G ,OD=3,
,OD=3, (cm)
(cm)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
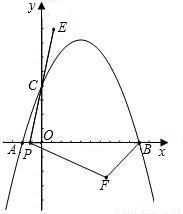
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省铁岭市中考数学试卷(解析版) 题型:解答题
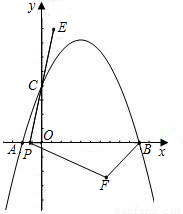
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《三角形》(03)(解析版) 题型:选择题

 米
米 米
米 +1)米
+1)米查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com