
ЎҫМвДҝЎҝЧгЗтИьЖЪјдЈ¬ДіЙМөкПъКЫТ»ЕъЧгЗтјНДоІбЈ¬ГҝұҫҪшјЫ40ФӘЈ¬№ж¶ЁПъКЫөҘјЫІ»өНУЪ44ФӘЈ¬ЗТ»сАыІ»ёЯУЪ30%.КФПъКЫЖЪјд·ўПЦЈ¬өұПъКЫөҘјЫ¶ЁОӘ44ФӘКұЈ¬ГҝМмҝЙКЫіц300ұҫЈ¬ПъКЫөҘјЫГҝХЗ1ФӘЈ¬ГҝМмПъКЫБҝјхЙЩ10ұҫЈ¬ПЦЙМөкҫц¶ЁМбјЫПъКЫ.ЙиГҝМмПъКЫОӘ![]() ұҫЈ¬ПъКЫөҘјЫОӘ
ұҫЈ¬ПъКЫөҘјЫОӘ![]() ФӘ.
ФӘ.
ЈЁ1Ј©ЗлЦұҪУРҙіц![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪәНЧФұдБҝ
Ц®јдөДәҜКэ№ШПөКҪәНЧФұдБҝ![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ2Ј©Ҫ«ЧгЗтјНДоІбПъКЫөҘјЫ¶ЁОӘ¶аЙЩФӘКұЈ¬ЙМөкГҝМмПъКЫјНДоІб»сөГөДАыИу![]() ФӘЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩФӘЈҝ
ФӘЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩФӘЈҝ
Ўҫҙр°ёЎҝЈЁ1Ј©![]() ЈЁ2Ј©өұx=52КұЈ¬wУРЧоҙуЦөОӘ2640.
ЈЁ2Ј©өұx=52КұЈ¬wУРЧоҙуЦөОӘ2640.
ЎҫҪвОцЎҝ
ЈЁ1Ј©КЫөҘјЫГҝЙПХЗ1ФӘЈ¬ГҝМмПъКЫБҝјхЙЩ10ұҫЈ¬ФтКЫөҘјЫГҝЙПХЗЈЁx-44Ј©ФӘЈ¬ГҝМмПъКЫБҝјхЙЩ10ЈЁx-44Ј©ұҫЈ¬ЛщТФy=300-10ЈЁx-44Ј©Ј¬И»әуАыУГПъКЫөҘјЫІ»өНУЪ44ФӘЈ¬ЗТ»сАыІ»ёЯУЪ30%И·¶ЁxөД·¶О§Ј»
ЈЁ2Ј©АыУГАыУГГҝұҫөДАыИуіЛТФПъКЫБҝөГөҪЧЬАыИуөГөҪw=ЈЁx-40Ј©ЈЁ-10x+740Ј©Ј¬ФЩ°СЛьұдРООӘ¶ҘөгКҪЈ¬И»әуАыУГ¶юҙОәҜКэөДРФЦКөГөҪx=52КұwЧоҙуЈ¬ҙУ¶шјЖЛгіцx=52Кұ¶ФУҰөДwөДЦөјҙҝЙЈ®
ЈЁ1Ј©УЙМвТвөГЈәy=300-10ЈЁx-44Ј©=-10x+740Ј¬
ГҝұҫҪшјЫ40ФӘЈ¬ЗТ»сАыІ»ёЯУЪ30%Ј¬јҙЧоёЯјЫОӘ52ФӘЈ¬јҙxЎЬ52Ј¬№КЈә44ЎЬxЎЬ52Ј¬
ЈЁ2Ј©w=ЈЁx-40Ј©ЈЁ-10x+740Ј©=-10ЈЁx-57Ј©2+2890Ј¬
өұxЈј57КұЈ¬wЛжxөДФцҙу¶шФцҙуЈ¬
¶ш44ЎЬxЎЬ52Ј¬ЛщТФөұx=52КұЈ¬wУРЧоҙуЦөЈ¬ЧоҙуЦөОӘ2640Ј¬
ҙрЈәҪ«ЧгЗтјНДоІбПъКЫөҘјЫ¶ЁОӘ52ФӘКұЈ¬ЙМөкГҝМмПъКЫјНДоІб»сөГөДАыИуwФӘЧоҙуЈ¬ЧоҙуАыИу2640ФӘЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
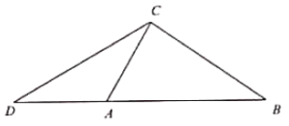
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘФЪ![]() ЦРЈ¬ЎПACB=90ЎгЈ¬
ЦРЈ¬ЎПACB=90ЎгЈ¬![]() Ј¬СУіӨұЯBAЦБөгDЈ¬К№AD=ACЈ¬БӘҪбCD.
Ј¬СУіӨұЯBAЦБөгDЈ¬К№AD=ACЈ¬БӘҪбCD.
ЈЁ1Ј©ЗуЎПDөДХэЗРЦөЈ»
ЈЁ2Ј©ИЎұЯACөДЦРөгEЈ¬БӘҪбBEІўСУіӨҪ»ұЯCDУЪөгFЈ¬Зу![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЎчABCКЗЦұҪЗИэҪЗРОЈ¬ЎПACB=90ЎгЈ¬өгAЈ¬CөДЧшұк·ЦұрОӘAЈЁ©Ғ3Ј¬0Ј©Ј¬CЈЁ1Ј¬0Ј©Ј¬tanЎПBAC=![]() Ј®
Ј®
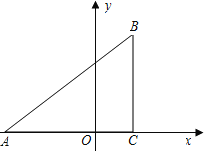
ЈЁ1Ј©Зу№эөгAЈ¬BөДЦұПЯөДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©ФЪxЦбЙПХТТ»өгDЈ¬Б¬ҪУBDЈ¬К№өГЎчADBУлЎчABCПаЛЖЈЁІ»°ьАЁИ«өИЈ©Ј¬ІўЗуөгDөДЧшұкЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬ИзPЈ¬Q·ЦұрКЗABәНADЙПөД¶ҜөгЈ¬Б¬ҪУPQЈ¬ЙиAP=DQ=mЈ¬ОККЗ·сҙжФЪХвСщөДmК№өГЎчAPQУлЎчADBПаЛЖЈҝИзҙжФЪЈ¬ЗлЗуіцөДmЦөЈ»ИзІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЛДХЕЖЛҝЛЕЖөДөгКэ·ЦұрКЗ2Ўў3Ўў4Ўў8Ј¬Ҫ«ЛьГЗПҙФИәуұіГжіҜЙП·ЕФЪЧАГжЙПЈ®
(1)ҙУЦРЛж»ъійИЎТ»ХЕЕЖЈ¬ЗуХвХЕЕЖөДөгКэКЗЕјКэөДёЕВКЈ»
(2)ҙУЦРПИЛж»ъійИЎТ»ХЕЕЖЈ¬ҪУЧЕФЩійИЎТ»ХЕЕЖЈ¬ЗуХвБҪХЕЕЖөДөгКэ¶јКЗЕјКэөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯ![]() өД¶ФіЖЦбОӘ
өД¶ФіЖЦбОӘ![]() Ј¬ЗТ№эөг
Ј¬ЗТ№эөг![]() Ј¬УРПВБРҪбВЫЈәўЩ
Ј¬УРПВБРҪбВЫЈәўЩ![]() Јҫ0Ј»ўЪ
Јҫ0Ј»ўЪ![]() Јҫ0Ј»ўЫ
Јҫ0Ј»ўЫ![]() Ј»ўЬ
Ј»ўЬ![]() Јҫ0.ЖдЦРХэИ·өДҪбВЫКЗЈЁ Ј©
Јҫ0.ЖдЦРХэИ·өДҪбВЫКЗЈЁ Ј©

A.ўЩўЫB.ўЩўЬC.ўЩўЪD.ўЪўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪТ»ёцІ»НёГчөДІјҙьАпЧ°УР4ёцұкУР![]() Ј¬2Ј¬3Ј¬4өДРЎЗтЈ¬ЛьГЗөДРОЧҙЎўҙуРЎЎўЦКөШНкИ«ПаН¬Ј¬РЎАоҙУІјҙьАпЛж»ъИЎіцТ»ёцРЎЗтЈ¬јЗПВКэЧЦОӘxЈ¬РЎХЕФЪКЈПВөД3ёцРЎЗтЦРЛж»ъИЎіцТ»ёцРЎЗтЈ¬јЗПВКэЧЦОӘyЈ¬ХвСщИ·¶ЁБЛөгQөДЧшұк(xЈ¬y).
Ј¬2Ј¬3Ј¬4өДРЎЗтЈ¬ЛьГЗөДРОЧҙЎўҙуРЎЎўЦКөШНкИ«ПаН¬Ј¬РЎАоҙУІјҙьАпЛж»ъИЎіцТ»ёцРЎЗтЈ¬јЗПВКэЧЦОӘxЈ¬РЎХЕФЪКЈПВөД3ёцРЎЗтЦРЛж»ъИЎіцТ»ёцРЎЗтЈ¬јЗПВКэЧЦОӘyЈ¬ХвСщИ·¶ЁБЛөгQөДЧшұк(xЈ¬y).
(1)»ӯКчЧҙНј»тБРұнЈ¬РҙіцөгQЛщУРҝЙДЬөДЧшұкЈ»
(2)ЗуөгQ(xЈ¬y)ВдФЪөЪ¶юПуПЮөДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
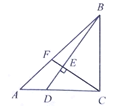
ЎҫМвДҝЎҝИзНјЈ¬![]() КЗөИСьЦұҪЗИэҪЗРОЈ¬
КЗөИСьЦұҪЗИэҪЗРОЈ¬![]() Ј¬
Ј¬![]() ОӘұЯ
ОӘұЯ![]() ЙПТ»өгЈ¬ЗТ
ЙПТ»өгЈ¬ЗТ![]() Ј¬Б¬Ҫб
Ј¬Б¬Ҫб![]() Ј¬№эөг
Ј¬№эөг![]() Чч
Чч![]() УЪөг
УЪөг![]() Ј¬Ҫ»
Ј¬Ҫ»![]() УЪөг
УЪөг![]() .Иф
.Иф![]() Ј¬Фт
Ј¬Фт![]() өДіӨОӘ______.
өДіӨОӘ______.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Ҫ«ҫШРОABCDСШAFХЫөюЈ¬К№өгDВдФЪBCұЯөДөгEҙҰЈ¬№эөгEЧчEGЎОCDҪ»AFУЪөгGЈ¬Б¬ҪУDGЈ®ёшіцТФПВҪбВЫЈәўЩDGЈҪDFЈ»ўЪЛДұЯРОEFDGКЗБвРОЈ»ўЫEG2ЈҪ![]() GFЎБAFЈ»ўЬөұAGЈҪ6Ј¬EGЈҪ2
GFЎБAFЈ»ўЬөұAGЈҪ6Ј¬EGЈҪ2![]() КұЈ¬BEөДіӨОӘ
КұЈ¬BEөДіӨОӘ![]() Ј¬ЖдЦРХэИ·өДұаәЕЧйәПКЗЈЁЎЎЎЎЈ©
Ј¬ЖдЦРХэИ·өДұаәЕЧйәПКЗЈЁЎЎЎЎЈ©

A.ўЩўЪўЫB.ўЩўЪўЬC.ўЩўЫўЬD.ўЩўЪўЫўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
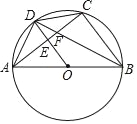
ЎҫМвДҝЎҝИзНјЈ¬ABКЗЎСOөДЦұҫ¶Ј¬өгCКЗФІЙПИОТвТ»өгЈ¬өгDКЗACЦРөгЈ¬ODҪ»ACУЪөгEЈ¬BDҪ»ACУЪөгFЈ¬ИфBFЈҪ1.25DFЈ¬ФтtanЎПABDөДЦөОӘЈЁЎЎЎЎЈ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com