
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上且点
边上且点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等.
的距离相等.
(1)利用尺规作图作出点![]() ,不写作法但保留作图痕迹.
,不写作法但保留作图痕迹.
(2)连接![]() ,若
,若![]() ,求∠B的度数.
,求∠B的度数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.

(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,请写出图中两对“等角三角形”.
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°。求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,若△ACD是等腰三角形,请直接写出∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,连接AD,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.
(1)求证:∠B=∠DAC.
(2)求证:AC=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,BD、CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,分别交AB、AC于E、F,则
,BD、CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,分别交AB、AC于E、F,则![]() 的周长为 ( )
的周长为 ( )

A.12B.13C.14D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
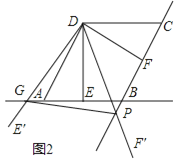
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.将∠EDF以点D为旋转中心旋转,其两边DE′,DF′分别与直线AB,BC相交于点G,P,连接GP,当△DGP的面积等于3![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC、△DCE均为等边三角形,当B、C、E三点在同一条直线上时,连接BD、AE交于点F,易证:△ACE≌△BCD.聪明的小明将△DCE绕点C旋转的过程中发现了一些不变的结论,让我们一起开启小明的探索之旅!

(探究一)如图2,当B、C、E三点不在同一条直线上时,小明发现∠BFE的大小没有发生变化,请你帮他求出∠BFE的度数.

(探究二)阅读材料:在平时的练习中,我们曾探究得到这样一个正确的结论:两个全等三角形的对应边上的高相等.例如:如图3,如果△ABC≌△A’B’C’,AD、A’D’分别是△ABC、△A’B’C’的边BC、B’C’上的高,那么容易证明AD=A’D’.小明带着这样的思考又有了新的发现:如图4,若连接CF,则CF平分∠BFE,请你帮他说明理由.

(探究三)在探究二的基础上,小明又进一步研究发现,线段AF、BF、CF之间还存在一定的数量关系,请你写出它们之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com