
分析 (1)先解方程组用含a的代数式表示x,y的值,再代入有关x,y的不等关系得到关于a的不等式求解即可;
(2)根据绝对值的定义即可得到结论;
(3)首先用含m的式子表示x和y,由于x、y的值是一个等腰三角形两边的长,所以x、y可能是腰也可能是底,依次分析即可解决,注意应根据三角形三边关系验证是否能组成三角形.
解答 解:(1)解$\left\{\begin{array}{l}3x-y=2a-5\\ x+2y=3a+3\end{array}\right.$得∴$\left\{\begin{array}{l}{x=a-1}\\{y=a+2}\end{array}\right.$,
∵若关于x、y的二元一次方程组$\left\{\begin{array}{l}3x-y=2a-5\\ x+2y=3a+3\end{array}\right.$的解都为正数,
∴a>1;
(2)∵a>1,∴|a+1|-|a-1|=a+1-a+1=2;
(3)∵二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,这个等腰三角形的周长为9,
∴2(a-1)+a+2=9,
解得:a=3,
∴x=2,y=5,不能组成三角形,
∴2(a+2)+a-1=9,
解得:a=2,
∴x=1,y=4,能组成等腰三角形,
∴a的值是2.
点评 主要考查了方程组的解的定义和不等式的解法.理解方程组解的意义用含m的代数式表示出x,y,找到关于x,y的不等式并用a表示出来是解题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
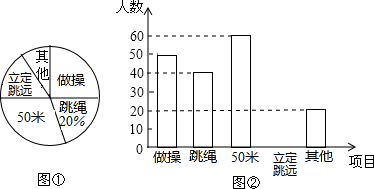 为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;
为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
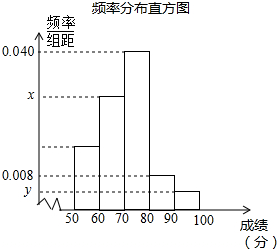 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图. | 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | |
| 3 | 70≤x<80 | 20 | 0.40 |
| 4 | 80≤x<90 | 0.08 | |
| 5 | 90≤x≤100 | 2 | b |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
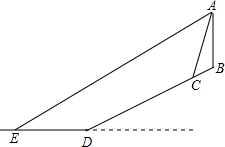 中考结束后,小明和好朋友一起前往三亚旅游.他们租住的宾馆AB坐落在坡度为i=1:2.4的斜坡上.某天,小明在宾馆顶楼的海景房A处向外看风景,发现宾馆前的 一座雕像C的俯角为76°(雕像的高度忽略不计),远处海面上一艘即将靠岸的轮船E的俯角为27°.已知雕像C距离海岸线D的距离CD为260米,与宾馆AB的水平距离为36米,问此时轮船E距离海岸线D的距离ED的长为( )(参考数据:tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.
中考结束后,小明和好朋友一起前往三亚旅游.他们租住的宾馆AB坐落在坡度为i=1:2.4的斜坡上.某天,小明在宾馆顶楼的海景房A处向外看风景,发现宾馆前的 一座雕像C的俯角为76°(雕像的高度忽略不计),远处海面上一艘即将靠岸的轮船E的俯角为27°.已知雕像C距离海岸线D的距离CD为260米,与宾馆AB的水平距离为36米,问此时轮船E距离海岸线D的距离ED的长为( )(参考数据:tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.| A. | 262 | B. | 212 | C. | 244 | D. | 276 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com