
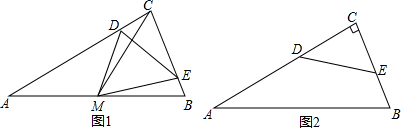
���� ��1��ֱ���������ε������ʽ���㼴�ɵó����ۣ�
��2��������1���Ľ�����ɶ���ʽ������ȷ�������ֵ��
��3���������������ε����ʵó�t�������CD��CD�����ù��ɶ������AB��DE������������ʽ���ɣ�
��� �⣺��1�����˶��ã�AD=2t��CE=t��
��AC=4��
��CD=4-2t��
��y=S��CDE=$\frac{1}{2}$CD��CE=$\frac{1}{2}$����4-2t����t=-t2+2t��0��t��2����
��2���ɣ�1��֪��y=-t2+2t=-��t-1��2+1��
��t=1ʱ��y���=1��
��3����ͼ2��
��M��AB�е㣬
��AM=CM=BM��
���A=��ACM��
��DE��CM��
���ACM+��CDF=90�㣬
���A+��CDF=90�㣬
�ߡ�A+��B=90�㣬
���B=��CDF��
�ߡ�ACB=��ECD��
���ABC�ס�EDC��
��$\frac{AB}{DE}=\frac{BC}{CD}=\frac{AC}{CE}$��
��CD=4-2t��CE=t��BC=2��AC=4��
��$\frac{2}{4-2t}=\frac{4}{t}$��
��t=$\frac{8}{5}$��
��CD=$\frac{4}{5}$��CE=$\frac{8}{5}$��
���ݹ��ɶ����ã�DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\frac{4\sqrt{5}}{5}$��
���������ȵã�CF��DE=CD��CE��
��CF=$\frac{CD��CE}{DE}$=$\frac{8\sqrt{5}}{25}$��
��Rt��ABC��AC=4��BC=2��
��AB=2$\sqrt{5}$����
CM=$\frac{1}{2}$AB=$\sqrt{5}$��
��MF=CM-CF=$\sqrt{5}$-$\frac{8\sqrt{5}}{25}$=$\frac{17\sqrt{5}}{25}$��
��S��DEM=$\frac{1}{2}$DE��MF=$\frac{1}{2}$��$\frac{4\sqrt{5}}{5}$��$\frac{17\sqrt{5}}{25}$=$\frac{34}{25}$��
���� �������������ۺ��⣬��Ҫ������ֱ�������ε����ʣ����ɶ��������������ε����ʺ��ж��������ε������ʽ�����ʱ��t�ǽⱾ��Ĺؼ�����һ���Ƚϼ��п������⣮


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-2����x+2��=0 | B�� | -2x2=0 | C�� | ��x-1��2=0 | D�� | ��x+1��2+2=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
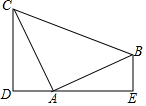 ��ͼ����֪AB��AC��AB=AC��DE����A����CD��DE��BE��DE������ֱ�Ϊ��D��E����˵��DE=DC+BE��
��ͼ����֪AB��AC��AB=AC��DE����A����CD��DE��BE��DE������ֱ�Ϊ��D��E����˵��DE=DC+BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������е��ı���ABCD�����Σ���sin$\frac{��BAD}{2}$��ֵΪ��������
��ͼ�������е��ı���ABCD�����Σ���sin$\frac{��BAD}{2}$��ֵΪ��������| A�� | $\frac{3}{4}$ | B�� | $\frac{3}{5}$ | C�� | $\frac{5}{3}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������·��A��B��C������ׯ����һ���������������������������������������һ����ó�г���ʹ��ó�г���������·�ľ�����ȣ���ü�ó�г�Ӧ���ڣ�������
��ͼ��������·��A��B��C������ׯ����һ���������������������������������������һ����ó�г���ʹ��ó�г���������·�ľ�����ȣ���ü�ó�г�Ӧ���ڣ�������| A�� | AC��BC���߸��ߵĽ��㴦 | B�� | AC��BC�������ߵĽ��㴦 | ||
| C�� | AC��BC���ߴ�ֱƽ���ߵĽ��㴦 | D�� | ��A����B���ڽ�ƽ���ߵĽ��㴦 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ӻ��������ڲ��Ź�� | B�� | ����������ˣ���������� | ||
| C�� | ��������� | D�� | ��һöӲ�ң����泯�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com