
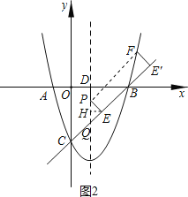
【题目】如图1,在平面直角坐标系中,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A(-1,0),点B,与y轴交于点C(0,-3),作直线BC.点P是抛物线的对称轴上的一个动点,P点到x轴和直线BC的距离分别为PD、PE.
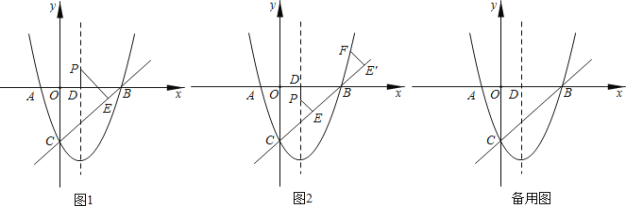
(1)求抛物线解析式;
(2)当P点运动过程中满足PE=PD时,求此时点P的坐标;
(3)如图2,从点B处沿着直线BC的垂线翻折PE得到FE',当点F在抛物线上时,求点P的坐标.
【答案】(1)y=x2-2x-3;(2)点P坐标为(1,2+2![]() )或(1,2-2
)或(1,2-2![]() );(3)点P坐标为(1,2+
);(3)点P坐标为(1,2+![]() )或(1,2-
)或(1,2-![]() ).
).
【解析】
(1)由点A、B关于对称轴:直线x=1对称,得B(3,0),再根据待定系数法,即可求解;
(2)易得直线BC解析式为:y=x-3,∠OCB=45°,从而得Q(1,-2),设P(1,t),则PD=|t|,PQ=|t+2|,结合PQ=![]() PD,即可求解;
PD,即可求解;
(3)分两种情况:①当点P(1,t)在点Q上方时,②当点P(1,t)在点Q下方时,分别进行求解即可.
(1)∵抛物线与x轴交于点A(-1,0)、点B,
∴点A、B关于对称轴:直线x=1对称,
∴![]() =1,解得:xB=3,
=1,解得:xB=3,
∴B(3,0)
∵抛物线y=ax2+bx+c经过点A、B、C(0,-3)
∴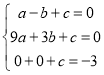 解得:
解得: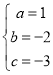 ,
,
∴抛物线解析式为y=x2-2x-3;
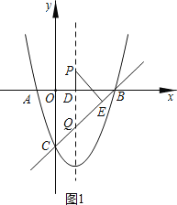
(2)如图1,记直线BC与对称轴交点为Q,
∵B(3,0),C(0,-3),
∴直线BC解析式为:y=x-3,∠OCB=45°,
∴Q(1,-2),
设P(1,t),则PD=|t|,PQ=|t+2|
∵PE⊥BC于点E,
∴∠PEQ=90°,
∵PQ∥y轴,
∴∠PQE=∠OCB=45°,
∴Rt△PEQ中,PQ=![]() PE
PE
∵PE=PD,
∴PQ=![]() PD,
PD,
∴PQ2=2PD2,
∴(t+2)2=2t2,
解得:t1=2+2![]() ,t2=2-2
,t2=2-2![]()
∴点P坐标为(1,2+2![]() )或(1,2-2
)或(1,2-2![]() );
);
(3)①如图2
连接PF,过点E作EH⊥PQ于点H,
∵∠PQE=45°,∠PEQ=90°,
∴△PEQ是等腰直角三角形,
∴PH=QH=EH=![]() PQ=
PQ=![]() ,
,
即点E向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位可得点P,
个单位可得点P,
∴xE=xP+![]() =
=![]() +2,yE=yP-
+2,yE=yP-![]() =
=![]() -1,即E(
-1,即E(![]() +2,
+2,![]() -1),
-1),
∵从点B处沿着直线BC的垂线翻折PE得到FE',
∴FE'⊥BC,FE'=PE,
∴FE'∥PE,
∴四边形PEE'F是平行四边形,
∴EE'∥PF,即EE'向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位可得PF,
个单位可得PF,
∵点B为EE'中点,
∴![]() =xB=3,yE'=-yE=1-
=xB=3,yE'=-yE=1-![]() ,
,
∴xE'=4-![]() ,
,
∴xF=xE'-![]() =3-t,yF=yE'+
=3-t,yF=yE'+![]() =2,即F(3-t,2),
=2,即F(3-t,2),
∵点F在抛物线上,
∴(3-t)2-2(3-t)-3=2,
解得:t1=2+![]() ,t2=2-
,t2=2-![]() ,
,
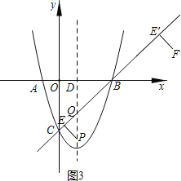
②如图3,当点P(1,t)在点Q下方时,t<-2,
则翻折后点F在直线BC下方,不可能在抛物线上,
综上所述,点P坐标为(1,2+![]() )或(1,2-
)或(1,2-![]() ).
).


科目:初中数学 来源: 题型:
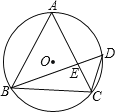
【题目】如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
(1)请找出图中的相似三角形,并加以证明;
(2)若∠D=45°,BC=2,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
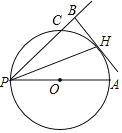
【题目】如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
(1)求证:HB是⊙O的切线;
(2)若HB=4,BC=2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民用水情况,小明在某小区随机抽查了20户家庭的月用水量,结果如下表:
月用水量(m3) | 4 | 5 | 6 | 8 | 9 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6m![]() B.平均数是5.8m
B.平均数是5.8m![]()
C.众数是6m![]() D.极差是6m
D.极差是6m![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测得某建筑物顶点O时俯角为30°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的水平飞行高度为45米,则这栋楼的高度是多少米?(结果保留根号)
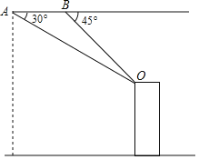
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】可以用如下方法求方程x2-2x-2=0的实数根的范围:利用函数y=x2-2x-2的图象可知,当x=0时,y<0,当x=-1时,y>0,所以方程有一个根在-1和0之间.
(1)参考上面的方法,求方程x2-2x-2=0的另一个根在哪两个连续整数之间;
(2)若方程x2-2x+c=0有一个根在0和1之间,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件,如果商场销售这批衬衫要获利润12000元,又使顾客获得更多的优惠,那么这种衬衫售价应定为多少元?
(1)设提价了![]() 元,则这种衬衫的售价为___________元,销售量为____________件.
元,则这种衬衫的售价为___________元,销售量为____________件.
(2)列方程完成本题的解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com