练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
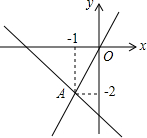
    1．如图，在平面直角坐标系中，一次函数y=k1x+b与正比例函数y=k2x的图象交于点A，则关于x的不等式k1x+b＜k2x的解集为x＞-1．

    分析 由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式k1x+b＜k2x解集．

    解答 解：两个条直线的交点坐标为（-1，-2），且当x＜-1时，直线y=k2x在y=k1x+b直线的下方，故不等式k1x+b＜k2x的解集为x＞-1．
    故答案为：x＞-1．

    点评 此题主要考查了一次函数与一元一次不等式，本题是借助一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

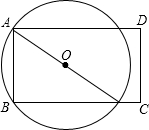    11．已知，如图，在矩形ABCD中，AB=6，BC=8，P点是线段BC上的任一动点，过点A、B、P作⊙O，设⊙O的半径为r，当⊙O与线段CD有且只有两个交点时，半径r的取值范围是$\frac{73}{16}$＜r≤5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

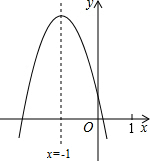    12．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①b2-4ac＜0；②4a+c＞2b；③3b+2c＜0；④4n（an+b）≤a，其中结论正确的个数是（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解不等式组$\left\{\begin{array}{l}{x+3＞0}\\{2（x-1）≥3}\end{array}\right.$，在数轴上表示解集，并判断x=$\sqrt{3}$是否为该不等式组的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．实验中学八年级（1）班50名学生参加期末考试，全班学生的数学成绩统计如表：
    成绩（分）71747880828385868890919294
    人数1235453784332
    请根据表中提供的信息解答下列问题：
    （1）该班学生这次考试数学成绩的众数是88分；
    （2）该班学生这次考试数学成绩的中位数是86分；
    （3）该班张华同学在这次考试中的数学成绩是83分，能不能说张华同学的数学成绩处于全班中游偏上水平？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知扇形的半径为3，扇形的圆心角是120°，则该扇形面积为3π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如果关于x的方程x2-2a-15=2（4a-1）x有一个根为-2，则a的值为$\frac{15}{14}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知直线y=5x+k与抛物线y=x2+3x+5交点的横坐标为1，则该直线与抛物线有几个交点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象，且过点A（2，1），那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$．

    查看答案和解析>>

    同步练习册答案