
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )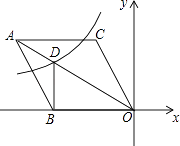
A.6 ![]()
B.﹣6 ![]()
C.12 ![]()
D.﹣12 ![]()
【答案】D
【解析】解:过点C作CE⊥x轴于点E,
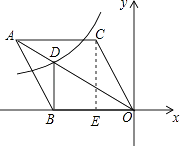
∵顶点C的坐标为(m,3 ![]() ),
),
∴OE=﹣m,CE=3 ![]() ,
,
∵菱形ABOC中,∠BOC=60°,
∴OB=OC= ![]() =6,∠BOD=
=6,∠BOD= ![]() ∠BOC=30°,
∠BOC=30°,
∵DB⊥x轴,
∴DB=OBtan30°=6× ![]() =2
=2 ![]() ,
,
∴点D的坐标为:(﹣6,2 ![]() ),
),
∵反比例函数y= ![]() 的图象与菱形对角线AO交D点,
的图象与菱形对角线AO交D点,
∴k=xy=﹣12 ![]() .
.
所以答案是:D.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y= ![]() 的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.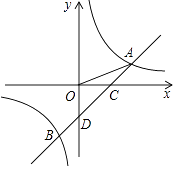
(1)求a,k的值及点B的坐标;
(2)直接写出不等式ax﹣1≥ ![]() 的解集;
的解集;
(3)在x轴上存在一点P,使得△POA与△OAC相似(不包括全等),请你求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是斜坡AC上的一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为4 m,钢丝绳BC的长度为5 m,AB⊥AD于点A,CD⊥AD于点D,若CD=2 m,则电线杆AB的高度是多少.(结果保留根号)
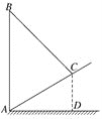
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实数范围内定义一种运算“*”,其运算法则为a*b=a2﹣ab.根据这个法则,下列结论中正确的是_______.(把所有正确结论的序号都填在横线上)
①![]() *
*![]() =2﹣
=2﹣![]() ;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=
;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=![]() ,x2=
,x2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题: 
(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有1080名学生,请估计该校训练后成绩为“A”等次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
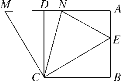
【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,![]() OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将![]() OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.
(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
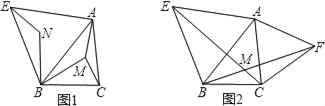
【题目】如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.
(1)求证:△AMB≌△ENB;
(2)若AM+BM+CM的值最小,则称点M为△ABC的费马点.若点M为△ABC的费马点,试求此时∠AMB、∠BMC、∠CMA的度数;
(3)小翔受以上启发,得到一个作锐角三角形费马点的简便方法:如图②,分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点.试说明这种作法的依据.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com