
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆O交AC于点D,交BC于点E,以点B为顶点作∠CBF,使得∠CBF=![]() ∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
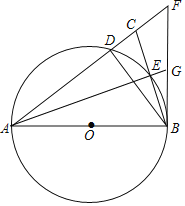
(1)求证:BF为⊙O的切线;(2)求证:ACBC=BDAG;(3)若BC=2![]() ,CD:CF=4:5,求⊙O的半径.
,CD:CF=4:5,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径OA=5.
【解析】
(1)由圆周角定理得出∠AEB=∠ADB=90°,得出AE⊥BC,由等腰三角形的性质得出∠BAE=∠CAE=![]() ∠BAC,证出∠BAE=∠CBF,证出∠ABF=90°,得出BF⊥OB,即可得出结论;
∠BAC,证出∠BAE=∠CBF,证出∠ABF=90°,得出BF⊥OB,即可得出结论;
(2)证出∠DBC=∠BAE,证明△BDC∽△ABG,得出![]() ,即可得出结论;
,即可得出结论;
(3)由(2)得:∠DBC=∠CBF,由角平分线性质得出![]() ,设BD=4x,则BF=5x,由勾股定理得:DF=
,设BD=4x,则BF=5x,由勾股定理得:DF=![]() =3x,证明△ABD∽△BFD,得出
=3x,证明△ABD∽△BFD,得出![]() ,求出AB=
,求出AB=![]() x,AD=
x,AD=![]() x,得出CD=AC﹣AD=
x,得出CD=AC﹣AD=![]() x,在Rt△BDC中,由勾股定理得出方程,解方程得x=
x,在Rt△BDC中,由勾股定理得出方程,解方程得x=![]() ,得出AB=10,即可得出⊙O的半径.
,得出AB=10,即可得出⊙O的半径.
(1)证明:∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴AE⊥BC,∠ABE+∠BAE=90°,
∵AB=AC,
∴∠BAE=∠CAE=![]() ∠BAC,
∠BAC,
∵∠CBF=![]() ∠BAC,
∠BAC,
∴∠BAE=∠CBF,
∴∠ABE+∠CBF=90°,
∴∠ABF=90°,
∴BF⊥OB,
∴BF为⊙O的切线;
(2)证明:∵∠DBC=∠CAE,∠BAE=∠CAE,
∴∠DBC=∠BAE,
∵∠BDC=90°=∠ABG,
∴△BDC∽△ABG,
∴![]() ,
,
∴ABBC=BDAG,
∵AB=AC,
∴ACBC=BDAG;
(3)解:由(2)得:∠DBC=∠CBF,
∴![]() ,
,
设BD=4x,则BF=5x,
由勾股定理得:DF=![]() =
=
∵∠BAD+∠ABD=90°,∠BAD+∠F=90°,
∴∠ABD=∠F,
∵∠ADB=∠BDF=90°,
∴△ABD∽△BFD,
∴![]() ,即
,即![]() ,
,
解得:AB=![]() x,AD=
x,AD=![]() x,
x,
∴AC=AB=![]() x,
x,
∴CD=AC﹣AD=![]() x,
x,
在Rt△BDC中,由勾股定理得:(4x)2+(![]() x)2=(2
x)2=(2![]() )2,
)2,
解得:x=![]() ,
,
∴AB![]() x=10,
x=10,
∴⊙O的半径OA=5.


科目:初中数学 来源: 题型:
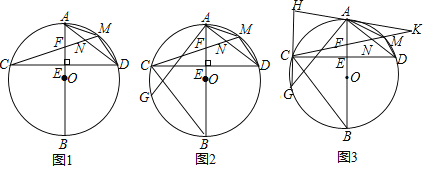
【题目】已知:AB为⊙O的直径,弦CD⊥AO,垂足为点E,连接AD,点N是AD上一点,连接CN交AE于点F,延长CN交⊙O与点M,连接AM,MD.
(1)如图1,求证:∠AMC=∠MCD+∠ADM;
(2)如图2,连接BC,过点A作AG⊥AD交⊙O与点G,求证:AG=BC;
(3)如图3,在(2)的条件下,AN=ND,延长CM至点K,MK=2MN=6,FE=3,连接KA,GC,并延长KA,GC交于点H,求HG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自习课上小明在准备完成题目:化简:( ![]() x2+6x+8)-(6x+8x2+2)发现系数“
x2+6x+8)-(6x+8x2+2)发现系数“ ![]() ” 印刷不清楚、
” 印刷不清楚、
(1)他把“ ![]() ”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2);
”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2);
(2)小明同桌看到他化简的结果说:“你猜错了,我看到该题标准答案的结果是常数。”请你通过计算说明原题中“ ![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
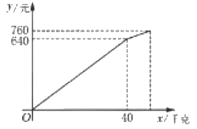
【题目】某水果店以每千克8元的价格收购苹果若干千克,销售了部分苹果后,余下的苹果以每千克降价4元销售,全部售完。销售金额y(元)与销售量x(千克)之间的关系如图所示。请根据图象提供的信息完成下列问题:
(1)降价前苹果的销售单价是 元/千克;
(2)求降价后销售金额y(元)与销售量x千克之间的函数解析式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=x+3与x轴、y轴分别交于点A、B,将直线AB向下平移与反比例函数![]() (x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=
(x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=![]() .
.
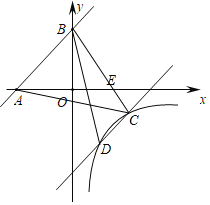
(1)求直线BC和反比例函数解析式;(2)连接BD,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于![]() MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
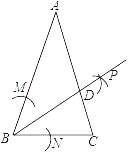
A. BDB. CDC. BD和ADD. CD和AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知Rt△ABC中,∠ACB=90°,AC=8,AB=10,点D是AC边上一点(不与C重合),以AD为直径作⊙O,过C作CE切⊙O于E,交AB于F.
(1)若⊙O半径为2,求线段CE的长;
(2)若AF=BF,求⊙O的半径;
(3)如图②,若CE=CB,点B关于AC的对称点为点G,试求G、E两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
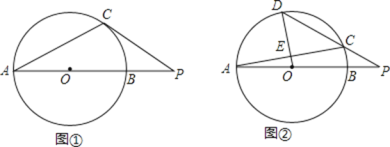
【题目】在![]() 中, AB为直径, C 为
中, AB为直径, C 为![]() 上一点。
上一点。
(1)如图 1. 过点 C 作 O 的切线 , 与 AB 的延长线相交于点 P, 若 ∠CAB=27°,求 ∠P 的大小;
(2)如图 2,D 为![]() 上一点 , 且 OD 经过 AC 的中点 E, 连接 DC 并延长 , 与 AB 的延长线相交于点 P, 若 ∠CAB=10°,求 ∠P 的大小.
上一点 , 且 OD 经过 AC 的中点 E, 连接 DC 并延长 , 与 AB 的延长线相交于点 P, 若 ∠CAB=10°,求 ∠P 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 公司
公司![]() 年使用自主研发生产的“
年使用自主研发生产的“![]() ”系列甲、乙、丙三类芯片共
”系列甲、乙、丙三类芯片共![]() 万块,生产了
万块,生产了![]() 万部手机,其中乙类芯片的产量是甲类芯片的
万部手机,其中乙类芯片的产量是甲类芯片的![]() 倍,丙类芯片的产量比甲、乙两类芯片产量的和还多
倍,丙类芯片的产量比甲、乙两类芯片产量的和还多![]() 万块.这些“
万块.这些“![]() ”芯片解决了该公司
”芯片解决了该公司![]() 年生产的全部手机所需芯片的
年生产的全部手机所需芯片的![]() .
.
(1)求![]() 年甲类芯片的产量;
年甲类芯片的产量;
(2)![]() 公司计划
公司计划![]() 年生产的手机全部使用自主研发的“
年生产的手机全部使用自主研发的“![]() ”系列芯片.从
”系列芯片.从![]() 年起逐年扩大“
年起逐年扩大“![]() ”芯片的产量,
”芯片的产量,![]() 年、
年、![]() 年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数
年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数![]() ,乙类芯片的产量平均每年增长的百分数比
,乙类芯片的产量平均每年增长的百分数比![]() 小
小![]() ,丙类芯片的产量每年按相同的数量递增.
,丙类芯片的产量每年按相同的数量递增.![]() 年到
年到![]() 年,丙类芯片三年的总产量达到
年,丙类芯片三年的总产量达到![]() 亿块.这样,
亿块.这样,![]() 年的
年的![]() 公司的手机产量比
公司的手机产量比![]() 年全年的手机产量多
年全年的手机产量多![]() ,求丙类芯片
,求丙类芯片![]() 年的产量及
年的产量及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com