
����Ŀ��2016��2��1�գ��ҹ����������Ƿ������ģ��ó������ű����ػ���ɹ�����5����һ������������Ԥ���������ͼ������ӵ���L�����䣬������ﵽA��ʱ����λ�ڵ���R���״�վ���AR�ľ�����6km������Ϊ42.4�㣻1���������B�㣬��ʱ�������Ϊ45.5��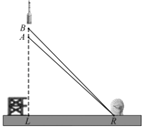
��1������̨���״�վ֮��ľ���LR��
��2������ö�����A��B��ƽ���ٶ��Ƕ��٣������ȷ��0.01����
���ο����ݣ�son42.4���0.67��cos42.4���0.74��tan42.4���0.905��sin45.5���0.71��cos45.5���0.70��tan45.5���1.02 ��
���𰸡�
��1��
�⣺��Rt��ALR�У�AR=6km����ARL=42.4�㣬
��cos��ARL= ![]() ����LR=ARcos��ARL=6��cos42.4���4.44��km����
����LR=ARcos��ARL=6��cos42.4���4.44��km����
�𣺷���̨���״�վ֮��ľ���LRΪ4.44km
��2��
�⣺��Rt��BLR�У�LR=4.44km����BRL=45.5�㣬
��tan��BRL= ![]() ����BL=LRtan��BRL=4.44��tan45.5���4.44��1.02=4.5288��km����
����BL=LRtan��BRL=4.44��tan45.5���4.44��1.02=4.5288��km����
�֡�sin��ARL= ![]() ����AL=ARsin��ARL=6��sin42.4���4.02��km����
����AL=ARsin��ARL=6��sin42.4���4.02��km����
��AB=BL��AL=4.5288��4.02=0.5088��0.51��km����
����ö�����A��B��ƽ���ٶȴ�Լ��0.51km/s��
����������1����������ֱ������������Ǻ�����ϵ�ó�LR=ARcos��ARL����𰸼��ɣ���2����������ֱ������������Ǻ�����ϵ�ó�BL=LRtan��BRL��������AL=ARsin��ARL�����AB��ֵ�������ó��𰸣�������Ҫ�����˽�ֱ�������ε�Ӧ�ã���ȷѡ��������Ǻ�����ϵ�ǽ���ؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����ǰ������ֱ�Ƕ����غ���һ��
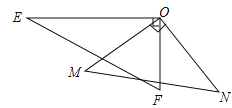
��1������EON=140��������MOF�Ķ�����
��2���Ƚ���EOM����FON�Ĵ�С����д�����ɣ�
��3������EON+��MOF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
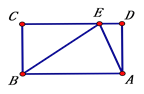
����Ŀ����ͼ������ABCD�У�AB=10��BC=6����EΪCD����һ�㡣
��1����AEƽ�֡�BEDʱ����DE�ij���
��2�����ܰѾ���ABCD��ij��ֱ��һ���ֳ����飬��ƴ��һ������������ܣ��ڱ���ͼ�л���ʾ��ͼ�����������νϳ��Խ��ߵij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=2AB=4��E��AD���е㣬һ���㹻������ǰ��ֱ�Ƕ������E�غϣ������ǰ��Ƶ�E��ת�����ǰ����ֱ�DZ߷ֱ�AB��BC�������ǵ��ӳ��ߣ��ڵ�M��N�����AEM=����0�㣼����90�㣩�����������ĸ����ۣ�
��AM=CN��
�ڡ�AME=��BNE��
��BN��AM=2��
��S��EMN= ![]() ��
��
������������ȷ�ĸ����ǣ�������
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
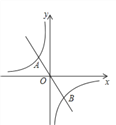
����Ŀ����ͼ,ֱ��y=kx(k<0)��˫����![]() ����A(x1��y1)��B(x2��y2)����,��3x1y2-5x2y1��ֵΪ __________.
����A(x1��y1)��B(x2��y2)����,��3x1y2-5x2y1��ֵΪ __________.
���𰸡�-6
������������������ߵ�A��x1��y1����B��x2��y2����˫����y��![]() �ϵĵ㣬
�ϵĵ㣬
��x1y1��x2y2����3����
��ֱ��y��kx��k��0����˫����y��![]() ���ڵ�A��x1��y1����B��x2��y2�����㣬
���ڵ�A��x1��y1����B��x2��y2�����㣬
��x1����x2��y1����y2����
��ԭʽ����3x1y1��5x2y2��9��15����6��
�ʴ�Ϊ����6��
�㾦�����⿼����Ƿ�����������һ�κ����Ľ������⣬�����������ĶԳ��ԣ����ݷ�����������ͼ�����ԭ��ԳƵó�x1����x2��y1����y2�ǽ�����Ĺؼ���
�����͡������
��������
15
����Ŀ��A��B�������180km�����ĸ��ٹ�·��ͨ����A��B���ؼ���ʻ�ij�;�ͳ�ƽ����������� 50%������A�ص�B�ص�ʱ�������� 1h .����ԭ����ƽ������Ϊxkm/h�������������з���Ϊ _____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AEƽ�֡�BAC����O�ڵ�E����BC�ڵ�D������E��ֱ��l��BC��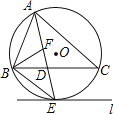
��1���ж�ֱ��l���O��λ�ù�ϵ����˵�����ɣ�
��2������ABC��ƽ����BF��AD�ڵ�F����֤��BE=EF��
��3���ڣ�2���������£���DE=4��DF=3����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��m��n��һԪ���η���x2+4x+3=0������ʵ��������|m|��|n|��������y=x2+bx+c��ͼ����A��m��0����B��0��n������ͼ��ʾ��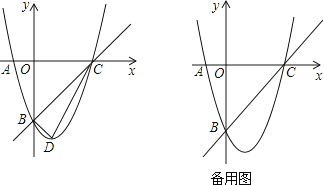
��1������������ߵĽ���ʽ��
��2���裨1���е���������x�����һ������Ϊ�����ߵĶ���ΪD���������C��D�����꣬���жϡ�BCD����״��
��3����P��ֱ��BC�ϵ�һ�����㣨��P�����B�͵�C�غϣ�������P��x��Ĵ��ߣ����������ڵ�M����Q��ֱ��BC�ϣ������PΪ ![]() ����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
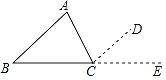
����Ŀ����֪����ABC����A����B����C֮��Ϊ���٣�Ϊʲô��
������A+��B+��C=180��
���ɣ�����ACD=��A�����ӳ�BC��E
�ߡ�ACD=���� ����������
AB��CD���� ����
���B=�� ������ ����
����ACB+��ACD+��DCE=180��
���ACB+�� ��+�� ��=180�㣨�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ��һЩƹ�����ƹ�����ģ��˽���Ϣ���£��ס��������̵��������ͬ��Ʒ�Ƶ�ƹ�����ƹ�����ģ�ƹ������ÿ������30Ԫ��ƹ����ÿ�ж���5Ԫ����Ǣ̸����ÿ��һ��������һ��ƹ�����ҵ�ȫ�������۵�9���Żݣ��ð�������5����ƹ�������ɺ�(��С��5��)���ʣ�
(1)������ƹ����x��ʱ�������Żݰ취��Ӧ�������Ԫ��(�ú�x�Ĵ���ʽ��ʾ)
(2)���Ҫ����15��ƹ����ʱ������ȥ������£������ȥ�ļ��̵깺��Ϊʲô��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com