
如图,已知抛物线y=﹣ x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
 |
解:(1)∵抛物线y=﹣ x2+bx+4的图象经过
x2+bx+4的图象经过 点A(﹣2,0),
点A(﹣2,0),
∴﹣ ×(﹣2)2+b×(﹣2)+4=0,解得:
×(﹣2)2+b×(﹣2)+4=0,解得: b=
b=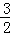 ,
,
∴抛物线解析式为 y=﹣ x2+
x2+ x+4,
x+4,
又∵y=﹣ x2+
x2+ x+4=﹣
x+4=﹣ (x﹣3)2+
(x﹣3)2+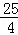 ,
,
∴对称轴为:直线x=3.
(2)在y=﹣ x2+
x2+ x+4中,令x=0,得y=4,∴C(0,4);
x+4中,令x=0,得y=4,∴C(0,4);
令y=0,即﹣ x2+
x2+ x+4=0,整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2, (第25题答案图)
x+4=0,整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2, (第25题答案图)
 ∴A(﹣2,0),B(8,0).
∴A(﹣2,0),B(8,0).
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式,得: ,
,
解得k= ,b=4,
,b=4,
∴直线BC的解析式为:y= x+4. (3)∵抛物线的对称轴为:x=3,可设点Q(3,t),则可求得:
x+4. (3)∵抛物线的对称轴为:x=3,可设点Q(3,t),则可求得:
AC= =
= =
= ,
,
AQ=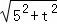 =
= ,
,
CQ= =
= .
.
i)当AQ=CQ时,
有 =
= ,解得t=0,∴Q1(3,0);
,解得t=0,∴Q1(3,0);
ii)当AC=AQ时,
有 =
=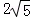 ,t2=﹣5,此方程无实数根,∴此时△ACQ不能构成等腰三角形;
,t2=﹣5,此方程无实数根,∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,
 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
△ABC中,AB=AC,∠BAC=α(0º<α<60º),将线段BC绕点B逆时针旋转60º得到线段BD.(本题图在答题卷上)
(1)如图1,直接写出∠AB D的大小(用含α的式子表示);
D的大小(用含α的式子表示);
(2)如图2,∠BCE=150º,∠ABE=60º,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45º,求α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图4,从A处观测C处的仰角为30°,从B处观测C处的仰角为45°,则从C处观测A、B两处的视角∠ACB为( )
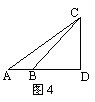 A.15° B.30° C.45° D.60°
A.15° B.30° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图5,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,
下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;
④∠DBF=2∠ABC.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com