

分析 (1)先求得tan∠A=2.从而得到PA=t,PD=QP=2t,最后依据PA+PN=4列方程求解即可;
(2)①当0<t<$\frac{2}{3}$时,EN=AE-PA-PN;当$\frac{2}{3}$≤t<2时,EN=AN-AE=PA+PN-AE;当t≥2时,EN=AP+PN-AE;
(3)①当0<t≤$\frac{4}{3}$时,S=正方形的面积;②当$\frac{4}{3}$<t≤2时.S=S正方形PQMN-S△FND;当2<t≤4时,S=梯形PQCD的面积;当4<t≤6时,S=△CQF的面积;当t>6时,S=0;
(4)如图9所示:建立坐标系可得到Q(2-t,2t,),M(2-3t,2t),然后分为OM=OQ,MO=MQ,QO=QM三种情况,接下来依据两点间的距离公式列方程求解即可;如图10所示:当Q在BC上时,MQ=QO=4,在Rt△BOQ中,依据勾股定理可求得QB的长,然后可求得t的值
解答 解:(1)如图1所示:
∵E是AD的中点,AD=4,
∴AE=2.
∵AE=2,BE=4,∠BEA=90°,
∴tan∠A=2.
又∵PA=t,
∴QP=2t.
∵PQMN为正方形,
∴PD=2t.
∴t+2t=4.
解得:t=$\frac{4}{3}$.
(2)①当0<t<$\frac{2}{3}$时,如图2所示:
∵由(1)可知PA=t,NP=2t.
∴EN=AE-PA-PN=2-t-2t=2-3t.
当$\frac{2}{3}$≤t<2时,如图3所示:
∵由(1)可知PA=t,NP=2t.
∴EN=AN-AE=PA+PN-AE=t+2t-2=3t-2.
当t≥2时,如图4所示: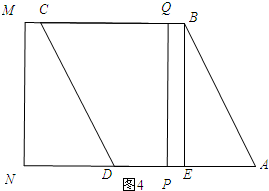
∵PA=t,PN=4,
∴EN=AP+PN-AE=t+4-2=t+2.
综上所述,EN=$\left\{\begin{array}{l}{2-3t(0<t<\frac{2}{3})}\\{3t-2(\frac{2}{3}≤t<2)}\\{t+2(t≥2)}\end{array}\right.$.
(3)①如图5所示:
当0<t≤$\frac{4}{3}$时,S=(2t)2=4t2;
②如图6所示:当$\frac{4}{3}$<t≤2时.
∵NA=3t,AD=4,
∴DN=3t-4.
∴FN=2ND=2(3t-4).
∴S=S正方形PQMN-S△FND=(2t)2-$\frac{1}{2}$×2×(3t-4)2=-5t2+24t-16.
当2<t≤4时,如图7所示:
∵CQ=CB+EA-PA=6-t,DP=AD-AP=4-t,
∴S=$\frac{1}{2}$×4×(6-t+4-t)=-4t+20.
当4<t≤6时,如图8所示: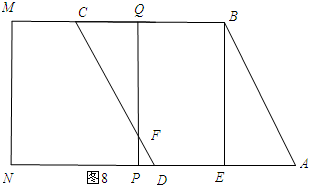
∵CQ=6-t,
∴QF=12-2t.
∴S=$\frac{1}{2}$CQ•QF=$\frac{1}{2}$×2×(6-t)2=t2-12t+36.
当t>6时,S=0.
综上所述S与t的函数为S=$\left\{\begin{array}{l}{4{t}^{2}(0<t≤\frac{4}{3})}\\{-5{t}^{2}+24t-16(\frac{4}{3}<t≤2)}\\{-4t+20(2<t≤4)}\\{{t}^{2}-12t+36(4<t≤6)}\\{0(t>2)}\end{array}\right.$.
(4)如图9所示: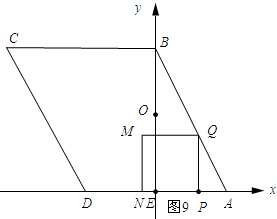
∵PA=t,PQ=QM=2t,
∴Q(2-t,2t,),M(2-3t,2t).
当OM=OQ时,由两点间的距离公式可知:(2-3t)2+(2-2t)2=(2-t)2+(2-2t)2.
整理得:-2t(4-4t)=0.
解得:t=1或t=0(舍去).
当MO=MQ时.(2-3t)2+(2-2t)2=(2t)2.
整理得:9t2-20t+8=0.
解得:t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$.
当QO=QM时(2-t)2+(2-2t)2=(2t)2.
整理得:t2-12t+8=0.
解得:t=6-2$\sqrt{7}$,t=6+2$\sqrt{7}$(舍去).
如图10所示:当MQ=QO=4时.
∵在Rt△BOQ中,QB=$\sqrt{Q{O}^{2}-O{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
∴PA+QB+EA=2$\sqrt{3}$+2即t=2+2$\sqrt{3}$.
综上所述,当t=2+2$\sqrt{3}$或t=6-2$\sqrt{7}$或t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$时,△MQO为等腰三角形.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了锐角三角形函数的定义、正方形的性质、正方形的面积、梯形的面积、三角形的面积,等腰三角形的定义,两点间的距离公式、一元二次方程、一元一次方程的解法,根据题意画出符合题意的图形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年江西省下期九年级第一次月考数学试卷(解析版) 题型:判断题
在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
(1)直接写出下列点的坐标:B1________,B2________,B3________;
(2)写出抛物线L2、L3的解析式,并写出其中一个解析式求解过程,再猜想抛物线Ln的顶点坐标
(3)设A1D1=k1·D1B1,A2D2=k2·D2B2,试判断k1与k2的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
已知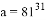 ,
,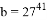 ,
,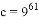 ,则
,则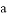 、
、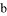 、
、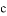 的大小关系是( )
的大小关系是( )
A. 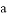 >
>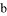 >
>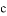 B.
B. 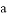 >
>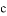 >
>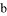 C.
C. 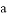 <
<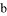 <
<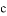 D.
D. 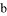 >
>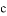 >
>
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点 A(-2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
在平面直角坐标系中,点 A(-2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com