
【题目】在平面直角坐标系中,已知直线y=﹣![]() x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,﹣![]() )B.(0,
)B.(0,![]() )C.(0,3)D.(0,4)
)C.(0,3)D.(0,4)
【答案】B
【解析】
设C(0,n),过C作CD⊥AB于D,先求出A,B的坐标,分别为(4,0),(0,3),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=4,则DB=5﹣4=1,BC=3﹣n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.
解:设C(0,n),过C作CD⊥AB于D,如图,
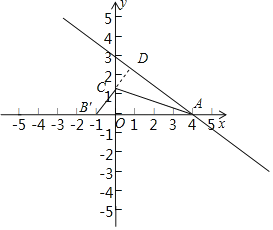
对于直线y=﹣![]() x+3,
x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3﹣n,
∴DA=OA=4,
∴DB=5﹣4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3﹣n)2,解得n=![]() ,
,
∴点C的坐标为(0,![]() ).
).
故选:B.


科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
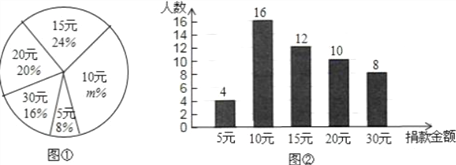
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如:![]() ,
,![]() ,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:![]() ,
, .
.
像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决下列问题:
(1)将![]() 分母有理化得 ;
分母有理化得 ;![]() 的有理化因式是 ;
的有理化因式是 ;
(2)化简:![]() = ;
= ;
(3)化简:![]() ……+
……+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
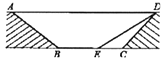
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.绳子的形状近似成了抛物线![]() ,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
(1)求立柱AB的长度;
(2)由于挂的衣服比较多,为了防止衣服碰到地面,小华用一根垂直于地面的立柱MN撑起绳子(如图2),MN的长度为1.85米,通过调整MN的位置,使左边抛物线F1对应函数的二次项系数为![]() ,顶点离地面1.6米,求MN离AB的距离.
,顶点离地面1.6米,求MN离AB的距离.
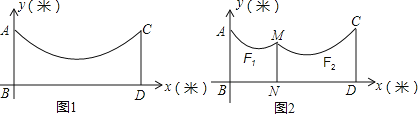
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.

(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com