
����Ŀ����֪OΪֱ��AB��һ�㣬��COE��ֱ�ǣ�OFƽ�֡�AOE.
(1)��ͼ�٣�����COF��34�㣬���BOE��________������COF��n�㣬���BOE��________����BOE���COF��������ϵΪ________________��
(2)������OE�Ƶ�O��ʱ����ת����ͼ�ڵ�λ��ʱ��(1)�С�BOE���COF��������ϵ�Ƿ���Ȼ��������˵�����ɣ�
(3)��ͼ���У�����COF��65�㣬�ڡ�BOE���ڲ��Ƿ����һ������OD��ʹ��2��BOD���AOF�ĺ͵��ڡ�BOE���BOD�IJ��һ�룿�����ڣ��������BOD�Ķ������������ڣ���˵�����ɣ�

���𰸡�(1)68�㣻2n�㣻��BOE��2��COF(2)��Ȼ����(3)����
��������
���⣨1�����ݽ�ƽ���ߵ����ʽ��ֱ�ǡ�ƽ�ǵĶ��弴�ɵõ������
��2����![]() �����ݽ�ƽ���ߵ����ʿɵ�
�����ݽ�ƽ���ߵ����ʿɵ�![]() �����ɵõ�
�����ɵõ�![]() ������
������![]() �ɵ�
�ɵ�![]() ���Ӷ��õ����ۣ�
���Ӷ��õ����ۣ�
��3������COF=65���ɵ���BOE=2��COF=130�������ɵõ���AOF�Ķ�������2��BOD+��AOF=![]() (��BOE-��BOD)��������ý��.
(��BOE-��BOD)��������ý��.
��1������COF��34��������BOE��68��������COF��m��������BOE��![]() ����������BOE=2��COF��
����������BOE=2��COF��
��2���������������£�
��![]()
��OF ƽ����AOE
��![]()
��![]()
��![]()
��![]()
���BOE=2��COF��
��3�����ڣ���BOD=16�����������£�
�ߡ�COF=65��
���BOE=2��COF=130��
���AOF=![]() (180��-��BOE)=25��
(180��-��BOE)=25��
��2��BOD+��AOF=![]() (��BOE-��BOD)
(��BOE-��BOD)
��2��BOD+25��=![]() (130��-��BOD)
(130��-��BOD)
���BOD=16��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��P�İ뾶Ϊ2��Բ��P��������y=![]() x2��1���˶�������P��x������ʱ��Բ��P������Ϊ
x2��1���˶�������P��x������ʱ��Բ��P������Ϊ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����������A��B��C������ֱ�ΪA��4��0����B��0��-3����C(2��-4����

��1������ͼ��ƽ��ֱ������ϵ�л�����ABC����x��ԳƵġ�A��B��C�������ֱ�д��A�䣬B�䣬C������ꣻ
��2������ABC����ƽ��5����λ���뻭��ƽ�ƺ�ġ�A��B��C�壬��д����A��B��C�������������ꣻ
��3�������2���еġ�ABC��ƽ�ƹ�������ɨ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�DE//AC����BC���ӳ����ڵ�E��EF��AB�ڵ�F.��֤����1��BC=CE����2��AD=CF.
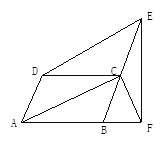
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�O��AC��һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F.
��1����֤��EO=FO����2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
��3����AC���ϴ��ڵ�O��ʹ�ı���AECF����������![]() �����B�Ĵ�С.
�����B�Ĵ�С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD�ǡ�ABC�Ľ�ƽ���ߣ���O����A��B��D���㣬����B��BE��AD������O�ڵ�E������ED��
��1����֤��ED��AC��
��2������AE����֤����ABCD=AEAC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����֪������ABC�У�AB=AC=10��BDƽ����ABC��CDƽ����ACB������D��EF��BC���ֱ�AB��AC��E��F���㣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��__________����AEF���ܳ���__________��
��2����ͼ2��������1��������ABC�У�AB=AC=10����Ϊ������ABCΪ���ȱ������Σ�AB=8��AC=10�������������䣬��ͼ�й���__________�����������Σ�EF��BE��CF֮���������ϵ��ʲô��֤����Ľ��ۣ��������AEF���ܳ���
��3����֪����ͼ3��D����ABC�⣬AB>AC����BDƽ����ABC��CDƽ����ABC�������ACG������D��DE��BC���ֱ�AB��AC��E��F���㣬��EF��BE��CF֮�����к�������ϵ�أ�ֱ��д�����۲�֤����

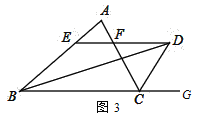
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Բ���ڽӵ���������ABC��Բ�İ뾶Ϊ10������ױ�BC�ij�Ϊ16����ô��ABC�����Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���³�����ڴ���װ�ˡ�����ʽ���ˡ�����A������ת����֧�㣬��E���������ε�����㣮����������ʱ������AEF���ֻ��������ͼ��ʾ��λ�ã�����AB��BC��EF��BC����AEF=135�㣬AB=AE=1.3�ף���ô�ʺϸõ��³���ij����߱�־��Ϊ�����˿��Ⱥ��Բ��ƣ��ο����ݣ�![]() ��1.4����������
��1.4����������
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com