
【题目】某商品的市场销售量y1(万件)和生产量y2(万件)都是该商品的定价x(元/件)的一次函数,其函数图象如图所示.
(1)分别求出y1、y2与x之间的函数表达式;
(2)若生产一件该商品成本为10元,未售出的商品一律报废.
①请解释点A的实际意义,并求出此时所获得的利润;
②该商品的定价为多少元时获得的利润最大,最大利润为多少万元?

【答案】(1)y1![]() x+65,y2
x+65,y2![]() x+10;(2)①当商品的定价为55元时,其市场销售量和生产量均为37.5万件,利润为1687.5万元;②当定价为60元时,获得最大利润为1700万元.
x+10;(2)①当商品的定价为55元时,其市场销售量和生产量均为37.5万件,利润为1687.5万元;②当定价为60元时,获得最大利润为1700万元.
【解析】
(1)利用待定系数法,结合图象上的点即可求解;
(2)①根据横轴与纵轴表示的意义解释点A的实际意义,用单件的利润×数量即可求出此时所获得的利润;
②设获得的利润为w万元,则有w=xy1-10y2,代入y1,y2,利用配方法求出顶点式,根据二次函数的性质解答即可.
依题意
(1)设y1=k1x+65,将x=130,y1=0代入得:k1![]() ,∴y1
,∴y1![]() x+65;
x+65;
把x=55代入y1![]() x+65得y1=37.5,
x+65得y1=37.5,
设y2=k2x+10,将x=55,y2=37.5代入得:k2![]() ,∴y2
,∴y2![]() x+10;
x+10;
(2)①当商品的定价为55元时,其市场销售量和生产量均为37.5万件;
(55﹣10)×37.5=1687.5万元,此时所获得的利润为1687.5万元.
②设获得的利润为w万元,则w=xy1﹣10y2=(![]() x+65)x﹣10(
x+65)x﹣10(![]() x+10),
x+10),
整理得:w![]() (x﹣60)2+1700,
(x﹣60)2+1700,
即当定价为60元时,获得最大利润为1700万元.


科目:初中数学 来源: 题型:
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的小正方形网格中,勤奋学习小组的同学画出了五边形
的小正方形网格中,勤奋学习小组的同学画出了五边形![]() 和五边形
和五边形![]() 则下列说法中,不正确的是( )
则下列说法中,不正确的是( )
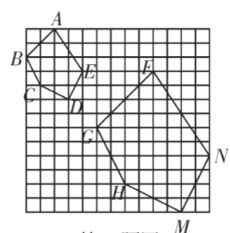
A.五边形![]()
![]() 五边形
五边形![]()
B.![]()
C.五边形![]() 的周长是五边形
的周长是五边形![]() 周长的
周长的![]() 倍.
倍.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
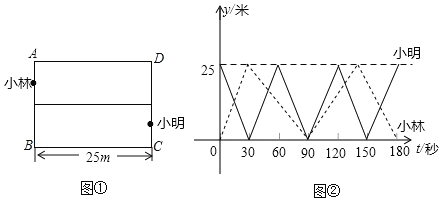
【题目】如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:
①小明游泳的平均速度小于小林游泳的平均速度;
②小明游泳的路程大于小林游泳的路程;
③小明游75m时,小林游了90m;
④小明与小林共相遇5次.
其中所有正确结论的序号是( )
A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
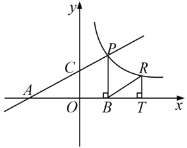
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥![]() 轴于B,且S△ABP=9.
轴于B,且S△ABP=9.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥![]() 轴于T,当△BRT与△AOC相似时,求点R的坐标.
轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)填空:
①当![]() 的度数为 时,四边形
的度数为 时,四边形![]() 为正方形;
为正方形;
②若![]() ,
,![]() ,则四边形
,则四边形![]() 的最大面积是 .
的最大面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与矩形ABCD的边AB,CD,AD相切,切点分别为E,F,G,边BC与⊙O交于M,N两点.下列五组条件中,能求出⊙O半径的有( )①已知AB,MN的长;②已知AB,BM的长;③已知AB,BN的长;④已知BE,BN的长;⑤已知BM,BN的长.

A.2组B.3组C.4组D.5组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边的中点,以点
是斜边的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
特例
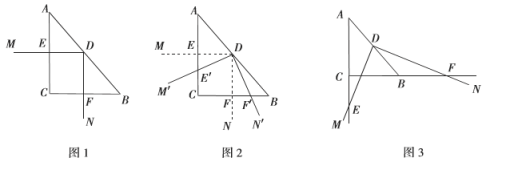
(1)如图1,若![]() ,不添加辅助线,图1中所有与
,不添加辅助线,图1中所有与![]() 相似的三角形为 ,
相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1的位置开始绕点
从图1的位置开始绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() ,如图2,当射线
,如图2,当射线![]() ,
,![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,以点
的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,则
,则![]() 的值为 .(用含
的值为 .(用含![]() 、
、![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com