Question

3．如图，圆锥母线长为2，底面半径为$\frac{2}{3}$，∠AOB=135°，经圆锥的侧面从A到B的最短距离为2$\sqrt{2-\sqrt{2}}$．

Answer 1

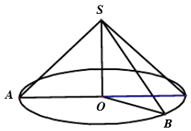
分析 根据题意，先画出圆锥的部分展开图，然后求出相应的弧长AB和展开后弧AB对应的圆心角，从而可以求出线段AB的长，本题得以解决．

解答 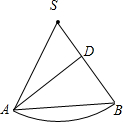解：如右图所示，是圆锥侧面展开的一部分，
∵圆锥母线长为2，底面半径为$\frac{2}{3}$，∠AOB=135°，
∴$\widehat{AB}=\frac{135π×\frac{2}{3}}{180}=\frac{π}{2}$，
作AD⊥SB于点D，
∵SA=SB=2，
∴展开的扇形所对的圆心角为$\frac{\frac{π}{2}}{2π×2}×360°=45°$，
∴在Rt△SAD中，AD=SD=$\sqrt{2}$，
∴BD=SB-SD=2-$\sqrt{2}$，
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}=\sqrt{（\sqrt{2}）^{2}+（2-\sqrt{2}）^{2}}$=$\sqrt{8-4\sqrt{2}}=2\sqrt{2-\sqrt{2}}$，
故答案为：2$\sqrt{2-\sqrt{2}}$．

点评 本题考查圆锥的计算、平面展开-最短路径问题，解题的关键是画出圆锥的平面展开图，利用两点之间线段最短解答，注意圆锥的母线是展开扇形的半径，圆锥的底面周长是展开扇形的弧长，找准对应量．