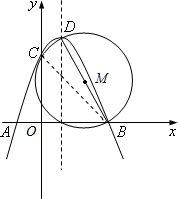
解:(1)∵抛物线y=ax
2+2x+3(a<0)交x轴于A、B两点,交y轴于点C,顶点为D.
∴对称轴为:x=-
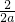
=-

,
∵当x=0时,y=3,
∴C的坐标为:(0,3),
∵D点的纵坐标为:y=

=
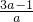
,
D点的坐标为:(-

,
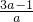
);…
(2)⊙M经过点C,
理由:连接BC,
∵a=-1,
∴抛物线为:y=-x
2+2x+3,
∴点D(1,4),点B(3,0),点C(0,3),
∴CD
2=2,BD
2=20,BC
2=18,
∴CD
2+BC
2=DB
2,
∴∠DCB=90°,
∵BD是直径,
∴∠BCD是直径所对的圆周角,
∴⊙M是经过点C;
(3)设P(x,-x
2+2x+3)
∵CD
2=2,BC
2=18,
∴CD=

,BC=3

,
①如图:若点P在对称轴的左侧,且△PQD∽△DCB,
则

,
即

,
解得:x
1=-2,x
2=1(舍去);
∴当x=-2时,y=-5;
∴P
1的坐标为(-2,-5);
②若点P在对称轴的左侧,且△PQD∽△BCD,

则

,
即

,
解得:x
3=

,x
4=1(舍去);
∴当x=

时,y=
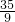
;
∴P
2的坐标为(

,
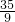
);
③若点P在对称轴的右侧,且△PQD∽△DCB,
则

,
即
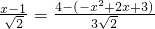
,
解得:x
5=4,x
6=1(舍去);
∴当x=4时,y=-5;
∴P
3的坐标为(4,-5);
④若点P在对称轴的右侧,且△PQD∽△BCD,
则

,
即

,
解得:x
7=

,x
8=1(舍去);
∴当x=

时,y=
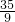
;
∴P
4的坐标为(

,
);
综上可得,点P的坐标为:P
1(-2,-5)或P
2(

,
)或P
3(4,-5)或P
4(

,
).…
分析:(1)由抛物线y=ax
2+2x+3(a<0)交x轴于A、B两点,交y轴于点C,顶点为D,根据二次函数的对称轴方程与顶点坐标的求解方法即可求得对称轴及D点的坐标,又由当x=0时,y=3,求得C点的坐标;
(2)首先求得点B,C,D的坐标,然后根据两点间的距离公式,求得BC,CD,BD的平方的值,即可得CD
2+BC
2=DB
2,由勾股定理的逆定理,可求得∠DCB=90°,又由直径所对的圆周角是直角,可得⊙M是经过点C;
(3)首先求得CD,BC,的长,然后分别从①若点P在对称轴的左侧,且△PQD∽△DCB,②若点P在对称轴的左侧,且△PQD∽△BCD,③若点P在对称轴的右侧,且△PQD∽△DCB,④若点P在对称轴的右侧,且△PQD∽△BCD去分析,根据相似三角形的对应边成比例,求得方程,解方程即可求得答案.
点评:此题考查了对称轴方程,顶点坐标的求解方法,圆的性质,相似三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想,方程思想与分类讨论思想的应用.

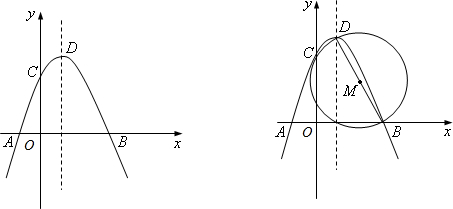
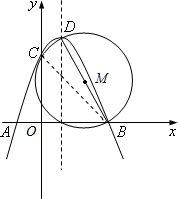 解:(1)∵抛物线y=ax2+2x+3(a<0)交x轴于A、B两点,交y轴于点C,顶点为D.
解:(1)∵抛物线y=ax2+2x+3(a<0)交x轴于A、B两点,交y轴于点C,顶点为D.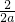 =-
=- ,
, =
=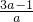 ,
, ,
,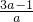 );…
);… ,BC=3
,BC=3 ,
, ,
, ,
,
 ,
, ,
, ,x4=1(舍去);
,x4=1(舍去); 时,y=
时,y=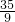 ;
; ,
,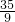 );
); ,
,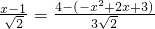 ,
, ,
, ,
, ,x8=1(舍去);
,x8=1(舍去); 时,y=
时,y=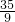 ;
; ,
,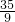 );
); ,
,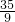 )或P3(4,-5)或P4(
)或P3(4,-5)或P4( ,
,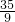 ).…
).…

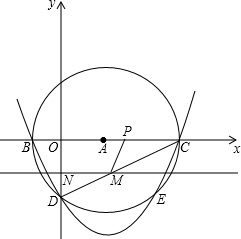
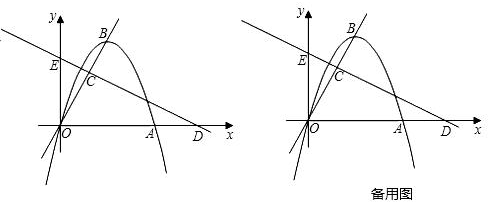
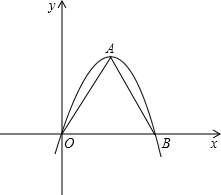 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.