
【题目】如图,点M为抛物线![]() 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

【答案】(1)![]() ,M(-1,-4);(2)
,M(-1,-4);(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据点A、B的坐标代入![]() ,求出b、c的值即可求出抛物线的解析式,进而求出M的坐标,(2)通过解析式可求出C点坐标,可知AO=OC根据∠DCA+∠ACE=∠OCE+∠ACE=
,求出b、c的值即可求出抛物线的解析式,进而求出M的坐标,(2)通过解析式可求出C点坐标,可知AO=OC根据∠DCA+∠ACE=∠OCE+∠ACE=![]() 可证明∠DCA=∠OCE,进而可知△DCA∽△ECO.
可证明∠DCA=∠OCE,进而可知△DCA∽△ECO.
即可求出AD:OE的值(3)分类讨论:当∠OEC=Rt∠时,由△DCA∽△ECO.可知∠ADC=∠OEC=Rt∠,由A、M、C三点坐标可求出三边长度,可知∠MCA=∠ADC=Rt∠
由∠DAC=∠CAM,可证明△ADC∽△ACM,即可求出AD的长;当∠ECO=Rt∠时,同理得∠ACD=Rt∠点D和点M重合,![]()
(1)把A(-3,0),B(1,0)代入![]() ,得
,得
![]() ∴
∴![]()
∴![]()
∴M(-1,-4)
(2)当x=0时,解得y=-3,
∴C(0,-3)
∵A(-3,0)
∴AO=OC=3,
∵∠AOC=![]()
∴∠OCA=![]() 且AC=
且AC=![]() OC
OC
∵△CDE为等腰直角三角形
∴∠DCE=![]() 且DC=
且DC=![]() EC
EC
∴∠DCA+∠ACE=∠OCE+∠ACE=![]()
∴∠DCA=∠OCE.
∴△DCA∽△ECO.
∴![]()
∴AD:OE=![]()
(3)①当∠OEC=Rt∠时,
∵△DCA∽△ECO,
∴∠ADC=∠OEC=Rt∠.
连接MC,∵A(-3,0),C(0,-3),M(-1,-4)
∴![]() ,
,![]() ,
,![]()
∴![]() ,即∠MCA=∠ADC=Rt∠
,即∠MCA=∠ADC=Rt∠
∵∠DAC=∠CAM,
∴△ADC∽△ACM,
∴![]()
∴![]()
②当∠ECO=Rt∠时,同理得∠ACD=Rt∠
∴点D和点M重合,∴![]()


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°,△COD固定不动,△AOB绕着O点逆时针旋转α°(0°<α<180° ),使两个三角形至少有一组边所在直线垂直,则α=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,BC=3,AB=4,![]() ,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
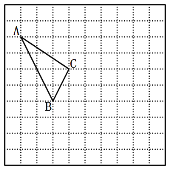
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),△ABC的顶点A,B的坐标分别为:(﹣4,3),(-2,﹣1).
(1)请在图中作出平面直角坐标系并写出点C的坐标;
(2)请作出将△ABC向下平移2个单位长度,再向右平移3个单位长度后的![]() ;并写出点C′的坐标.
;并写出点C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长相等的下列两种正多边形的组合,不能作平面镶嵌的是( )
A.正方形与正三角形B.正五边形与正三角形
C.正六边形与正三角形D.正八边形与正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com