
分析 (1)设甲种油茶树苗每株的价格为x元,则乙两种油茶树苗每株的价格为x+3元,根据购买5株甲种树苗的费用与购买8株乙种树苗的费用刚好相同列出方程解答即可;
(2)设购买甲种树苗a株,乙种树苗则购买(1000-a)株,根据两种树苗共用5600元建立方程求出其解即可;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,根据条件建立不等式和W与b的函数关系式,由一次函数的性质就可以得出结论.
解答 解:(1)设种油茶树苗每株的价格为x元,则乙两种油茶树苗每株的价格为x-3元,由题意得
5x=8(x-3)
解得:x=8
x-3=5
答:甲种油茶树苗每株的价格为8元,则乙两种油茶树苗每株的价格为5元;
(2)设甲购买了a株,乙购买了(1000-a)株,由题意得
8a+5(1000-a)=5600,
解得:a=200,
乙种树苗购买株数为:1000-200=800株.
答:甲种树苗200株,乙种树苗购买800株;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,由题意得
90%b+95%(1000-b)≥1000×92%,
∴b≤600.
W=5b+8(1000-b)=-3b+8000,
∴k=-3<0,
∴W随b的增大而减小,
∴b=600时,W最低=6200元.
答:购买甲种树苗600株,乙种树苗400株费用最低,最低费用是6200元.
点评 本题考查了列一元一次方程的实际运用,一元一次不等式解实际问题的运用,一次函数的解析式的运用,解答时由方程组求出两种树苗的单价是关键.


科目:初中数学 来源: 题型:填空题
 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=90°,则该圆锥的母线l长为8cm.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=90°,则该圆锥的母线l长为8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
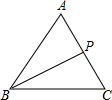 如图,在边长为1的正三角形ABC中,P是AC边上的一个动点,(不与两端重合),设PC=x,△ABP的面积为S
如图,在边长为1的正三角形ABC中,P是AC边上的一个动点,(不与两端重合),设PC=x,△ABP的面积为S查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18x=24(40-x) | B. | 2×18x=24(40-x) | C. | 24x=18(40-x) | D. | 18x=2×24(40-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com