
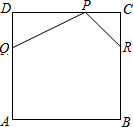
 ��ͼ��������ABCD��һ�ű߳�Ϊ12���ֵ�Ƥ�Ƥ��ʦ�����ڴ�Ƥ�������ڵĽ���ֱ����¡�PDQ���PCR��õ�һ�������PQABR������PD=2DQ��PC=RC����P��Q��
��ͼ��������ABCD��һ�ű߳�Ϊ12���ֵ�Ƥ�Ƥ��ʦ�����ڴ�Ƥ�������ڵĽ���ֱ����¡�PDQ���PCR��õ�һ�������PQABR������PD=2DQ��PC=RC����P��Q������ ��1������������ʾ��PD���Ӷ��õ���PDQ�������
��2���ֱ����������ABCD���������PDQ����PCR��������������������ε���������ȷ����ȡ��ֵʱ��xֵ��
��� �⣺��1����DQ=x���֣�
��PD=2DQ=2x���֣�
��S��PDQ=$\frac{1}{2}$x��2x=x2��ƽ�����֣���
��2����PD=2x���֣�CD=12���֣�
��PC=CR=12-2x�����֣���
��S�����PQABR=S������ABCD-S��PDQ-S��PCR
=122-x2-$\frac{1}{2}$��12-2x��2
=144-x2-$\frac{1}{2}$��144-48x+4x2��
=144-x2-72+24x-2x2
=-3x2+24x+72
=-3��x2-8x+42��+72+3��16
=-3��x-4��2+120��
�ʵ�x=4ʱ�������PQABR��������Ϊ120ƽ�����֣�
���� �������ı����ۺ��⣬��Ҫ����������������ļ��㣬���������ļ��㷽�����Ȿ��Ĺؼ��������ε�����ļ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2a-b����2a+b�� | B�� | ��x+2y����-2y+x�� | C�� | ��2a+b����a-2b�� | D�� | ��-x-y����-x+y�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
���Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�ص�һ������������ͼ��ʾ�����Ÿ�Ϊ6�ף�����BC���¶�Ϊ1��1��Ϊ�˷��������Ƴ������ţ��йز��ž��������¶ȣ�ʹ��������¶�Ϊ1��$\sqrt{3}$��
ij�ص�һ������������ͼ��ʾ�����Ÿ�Ϊ6�ף�����BC���¶�Ϊ1��1��Ϊ�˷��������Ƴ������ţ��йز��ž��������¶ȣ�ʹ��������¶�Ϊ1��$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���$y=\frac{1}{x}$��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn-1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An-1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA2���ڽ�������B1C1D1E2���ܳ���Ϊl1����P2A1A2���ڽ�������B2C2D2E2���ܳ���Ϊl2��������PnAn-1An���ڽ�������BnCnDnEn���ܳ���Ϊln�����ú�n��ʽ�ӱ�ʾl1+l2+l3+��+lnΪ��������
��ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���$y=\frac{1}{x}$��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn-1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An-1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA2���ڽ�������B1C1D1E2���ܳ���Ϊl1����P2A1A2���ڽ�������B2C2D2E2���ܳ���Ϊl2��������PnAn-1An���ڽ�������BnCnDnEn���ܳ���Ϊln�����ú�n��ʽ�ӱ�ʾl1+l2+l3+��+lnΪ��������| A�� | $\frac{8\sqrt{n}}{3}$ | B�� | 2$\sqrt{n}$ | C�� | $\frac{4\sqrt{n}}{3}$ | D�� | $\frac{2\sqrt{n}}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com