
 反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.
反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2. 分析 求出直线y=x+1与直线y=-x的交点坐标,由反比例函数与一次函数均关于直线y=-x对称,结合点A的坐标即可求出另一交点坐标,再根据两函数图象的上下位置关系结合两交点的横坐标即可得出不等式的解集.
解答 解:令y=x+1=-x,
解得:x=-$\frac{1}{2}$,y=-x=$\frac{1}{2}$.
∵反比例函数y=$\frac{6}{x}$和一次函数y=x+1的图象均关于直线y=-x对称,
∴反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交点关于点(-$\frac{1}{2}$,$\frac{1}{2}$)对称,
∴另一交点的坐标为(-$\frac{1}{2}$×2-2,$\frac{1}{2}$×2-3),即(-3,-2).
观察函数图象可知:当-3<x<0或x>2时,反比例函数图象在一次函数图象下方,
∴不等式$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.
故答案为:2;-3<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题以及函数图象,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依次A、B、C、D、E、F、C、G、A这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )| A. | D点 | B. | E点 | C. | F点 | D. | G点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
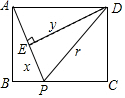 如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )| A. | 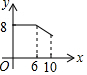 | B. | 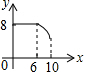 | C. |  | D. | 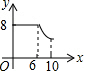 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com