
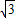 的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是 .
的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是 .
 ,
, ∠ABC=30°,∠EAO=30°,
∠ABC=30°,∠EAO=30°,
 ;
;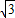 ;
;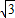 ,根据切线长定理可得,AB=BC=AC,
,根据切线长定理可得,AB=BC=AC,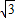 .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2011-2012学年广东省汕头市潮南区砺青中学九年级(上)第二次月考数学试卷(解析版) 题型:选择题
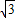 的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )
的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )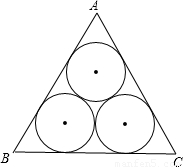




查看答案和解析>>
科目:初中数学 来源:2012年北京市中考数学模拟试卷(一)(解析版) 题型:选择题
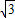 的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )
的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )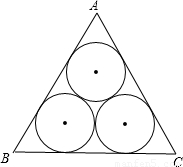
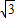
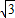
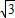

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《锐角三角函数》(01)(解析版) 题型:选择题
 的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )
的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是( )




查看答案和解析>>
科目:初中数学 来源:2010年中考复习—填空题汇总1(西湖区数学教研员提供)(解析版) 题型:填空题
 的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是 .
的圆两两外切,且△ABC的每一边都与其中的两个圆相切,那么△ABC的周长是 .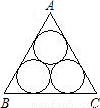
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com