
 将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1).
将n个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5,…是正方形对角线的交点,那么阴影部分面积之和等于$\frac{1}{4}$(n-1). 分析 根据题意可得,阴影部分的面积是正方形的面积的$\frac{1}{4}$,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和,问题得解.
解答 解:由题意可得阴影部分面积等于正方形面积的$\frac{1}{4}$,即是$\frac{1}{4}$.
n个这样的正方形重叠部分(阴影部分)的面积和为$\frac{1}{4}$×(n-1)=$\frac{1}{4}$(n-1).
故答案为:$\frac{1}{4}$(n-1).
点评 此题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.


科目:初中数学 来源: 题型:填空题
 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则线段EF的最小值为4$\sqrt{3}$.
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则线段EF的最小值为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:
如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,有一宽度为1的长方形纸带,平行于y轴,在x轴的正半轴上移动,交x轴的正半轴于点A、D,两边分别交函数y1=$\frac{1}{x}$(x>0)与y2=$\frac{3}{x}$(x>0)的图象于B、F和E、C,若四边形ABCD是矩形,则A点的坐标为($\frac{1}{2}$,0).
如图,在平面直角坐标系xOy中,有一宽度为1的长方形纸带,平行于y轴,在x轴的正半轴上移动,交x轴的正半轴于点A、D,两边分别交函数y1=$\frac{1}{x}$(x>0)与y2=$\frac{3}{x}$(x>0)的图象于B、F和E、C,若四边形ABCD是矩形,则A点的坐标为($\frac{1}{2}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
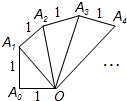 如图是由一系列直角三角形组成的螺旋形,OA=OA1=OA2=…OAn=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.
如图是由一系列直角三角形组成的螺旋形,OA=OA1=OA2=…OAn=1,则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com