
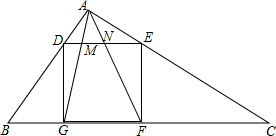
 如图,在Rt△ABC中,∠BAC=90°,四边形DEFG为内接于△ABC的正方形,AG、AF交DE于点M、N,若$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,求DM:MN:NE.
如图,在Rt△ABC中,∠BAC=90°,四边形DEFG为内接于△ABC的正方形,AG、AF交DE于点M、N,若$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,求DM:MN:NE. 分析 根据四边形DEFG为正方形,得到DG=GF=EF,BE∥GF,根据相似三角形的性质得到$\frac{DM}{BG}$=$\frac{AM}{AG}$,$\frac{NM}{GF}$=$\frac{AM}{AG}$=$\frac{AN}{AF}$,$\frac{AN}{AF}$=$\frac{EN}{CF}$,等量代换得到$\frac{DM}{BG}$=$\frac{MN}{GF}$=$\frac{NE}{CF}$,推出DM:MN:NE=BG:GF:CF,根据相似三角形的性质得到$\frac{BG}{DG}$=$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,同理$\frac{EF}{CF}$=$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,于是得到结论.
解答 解:∵四边形DEFG为正方形,
∴DG=GF=EF,BE∥GF,
∴△ADM∽△ABG,△AMN∽△AGF,△ANE∽△ACF,
∴$\frac{DM}{BG}$=$\frac{AM}{AG}$,$\frac{NM}{GF}$=$\frac{AM}{AG}$=$\frac{AN}{AF}$,$\frac{AN}{AF}$=$\frac{EN}{CF}$,
∴$\frac{DM}{BG}$=$\frac{MN}{GF}$=$\frac{NE}{CF}$,
∴DM:MN:NE=BG:GF:CF,
∵∠DGB=∠BAC=90°,∠B=∠B,
∴△DBG∽△ABC,
∴$\frac{BG}{DG}$=$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,
同理$\frac{EF}{CF}$=$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,
∴$\frac{BG}{GF}$=$\frac{GF}{CF}$=$\frac{{x}^{2}}{{y}^{2}}$,
∴DM:MN:NE=BG:GF:CF=x4:x2y2:y4.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 有一个角为50°的两个等腰三角形 | B. | 邻边之比为1:3的平行四边形 | ||
| C. | 有一个角为30°的两个菱形 | D. | 底角为40°的两等腰梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,-a,b,-b按照从小到大的顺序排列( )
a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,-a,b,-b按照从小到大的顺序排列( )| A. | -b<-a<a<b | B. | a<-b<b<-a | C. | -b<a<-a<b | D. | a<-b<-a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com