
【题目】如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( ) 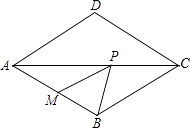
A.6 ![]()
B.3 ![]()
C.9
D.4.5
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
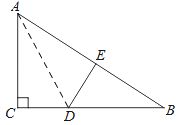
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为 . 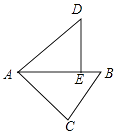
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( ) 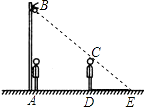
A.4米
B.5.6米
C.2.2米
D.12.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 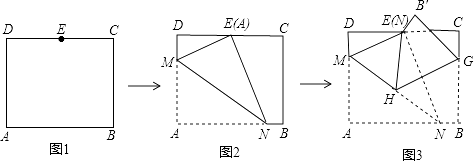
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
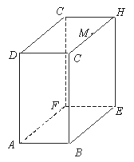
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线l1:y=x2﹣4的图象与x轴交于A,C两点,抛物线l2与l1关于x轴对称.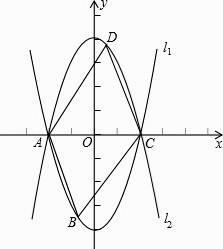
(1)直接写出l2所对应的函数表达式;
(2)若点B是抛物线l2上的动点(B与A,C不重合),以AC为对角线,A,B,C三点为顶点的平行四边形的第四个顶点为D,求证:D点在l2上.
(3)当点B位于l1在x轴下方的图象上,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它面积的最值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com