Question

5．如图，AB∥CD，∠E+∠G=∠H，则∠A+∠B+∠C+∠D+∠F的度数为360°．

Answer 1

分析 先延长AE，DG交于点Q，根据∠A+∠D=∠Q，∠B+∠H+∠C=360°，以及∠Q=∠AEF+∠DGF-∠F，可得∠A+∠D=∠AEF+∠DGF-∠F，即∠F=∠AEF+∠DGF-（∠A+∠D），再根据∠AEF+∠DFG=∠H，可得∠A+∠B+∠C+∠D+∠F=∠B+∠C+∠H，据此得出结论．

解答 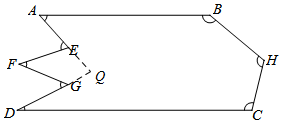解：如图所示，延长AE，DG交于点Q，
由题可得，∠A+∠D=∠Q，∠B+∠H+∠C=360°，
又∵∠Q=∠AEF+∠DGF-∠F，
∴∠A+∠D=∠AEF+∠DGF-∠F，
即∠F=∠AEF+∠DGF-（∠A+∠D），
又∵∠AEF+∠DFG=∠H，
∴∠A+∠B+∠C+∠D+∠F=∠A+∠B+∠C+∠D+∠AEF+∠DGF-（∠A+∠D）
=∠B+∠C+∠H
=360°，
故答案为：360°．

点评 本题主要考查了平行线的性质，解决问题的关键是作辅助线，依据两直线平行，同旁内角互补进行计算求解．