
����Ŀ����ͼ������ABCD����ƽ��ֱ������ϵ�У�����AD����x����, ֱ��MN: y=x��8��x��ĸ�������ÿ��2����λ�ij���ƽ��,����ƽ�ƹ����и�ֱ�߱�����ABCD�ı߽صõ��߶γ���Ϊm,ƽ��ʱ��Ϊt, m��t�ĺ���ͼ����ͼ2��ʾ.

(1)��AB=6
�ٵ�A������Ϊ_____________,����ABCD�����Ϊ____________.
����a, b��ֵ;
(2)��AB=4����ƽ�ƹ�����,��ֱ��MNɨ������ABCD����� S�� t�ĺ�����ϵʽ,��д���Ա���t��ȡֵ��Χ.
���𰸡���1���٣�2��0����48����a=6![]() ��b=10����2��
��b=10����2�� .
.
��������
��1���������M������Ϊ��8��0��������ͼ2�ɵÿ�ʼƽ��3����M�����A������AM=6��OA=2��ƽ��7����M�����D������AD=![]() ���ɴ˿���õ�A������;���ABCD������������ͼ2������������λ�ã�ֱ��MN����B�͵�C��Ȼ��ͼ�Σ����ֱ��ƽ�Ƶ��ٶȣ��Ӷ����a��b��ֵ��
���ɴ˿���õ�A������;���ABCD������������ͼ2������������λ�ã�ֱ��MN����B�͵�C��Ȼ��ͼ�Σ����ֱ��ƽ�Ƶ��ٶȣ��Ӷ����a��b��ֵ��
��2���ɸ�����Ŀ�е�ͼ1��ͼ2��ƽ�Ʒ�Ϊ�ĸ��Σ�Ȼ������������ĸ�����ֱ��MN��x�ύ������꣬�ó�����ɨ�����ֵ�ͼ�Σ�Ȼ��ֱ����ɨ�����ֵ����.
�⣺��1���ٶ�ֱ��y=x��8����y=0����x��8=0����ã�x=8�����M������Ϊ��8��0����
����ͼ2�ɵÿ�ʼƽ��3����M�����A������AM=6��OA=2��ƽ��7����M�����D������AD=![]() ����A������Ϊ��2��0��������ABCD�����Ϊ6��8=48��
����A������Ϊ��2��0��������ABCD�����Ϊ6��8=48��
������ͼ1��ʾ����ֱ��MN������Bʱ��ֱ��MN��DA�ڵ�E��

�ߵ�A������Ϊ��2��0����AB=6�����B������Ϊ��2��6����
��ֱ��ME�Ľ���ʽΪy=x+c��
����B���������ã�2+c=6����c=4��
��ֱ��ME�Ľ���ʽΪy=x+4��
��y=0����ã�x+4=0�����x=��4��
���E����������4��0����
��BE=![]() ��
��
��a=6![]() ��
��
����ͼ2��ʾ����ֱ��MN������Cʱ��ֱ��MN��x���ڵ�F��

�ߵ�D������Ϊ����6��0�������C������Ϊ����6��6����
��MF�Ľ���ʽΪy=x+d��������6��6������ã���6+d=6�����d=12��
��ֱ��MF�Ľ���ʽΪy=x+12��
��y=0�����x+12=0�����x=��12��
���F����������12��0����
��b=7+6��2=10��
��2����������е�ͼ1��ͼ2���ɽ�ֱ��MN��ƽ�ư���ʱ���Ϊ�ĸ��Σ��ٴӳ�ʼλ��ƽ�Ƶ���A����ӣ���ֱ��MN��x��Ľ�����AE֮�ڣ���ֱ��MN��x��Ľ�����ED֮�ڣ���ֱ��MN��x��Ľ�����DG֮�ڣ�������G������ͼ��ʾ.

��0��t��3ʱ��ֱ��MN���ڽ٣���ʱֱ��MN�����ABCDû�н��㣬����S=0��
��3<t<5ʱ��ֱ��MN���ڽڣ���ʱֱ��MNɨ������ABCD�IJ���Ϊһ��С����ֱ�������Σ����������ε�����Ϊ2t��6���������Ϊ![]() ��
��
��5��t��7ʱ��ֱ��MN���ڽۣ���ʱֱ��MNɨ������ABCD�IJ���Ϊһ��ֱ�����Σ��ϵ�Ϊ2t��10���µ�Ϊ2t��6����Ϊ4���������Ϊ![]() ��
��
��7��t��9ʱ��ֱ��MN���ڽܣ���ʱֱ��MNɨ������ABCD�IJ���Ϊ����ABCD��ȥ���Ͻǵ�С����ֱ�������Σ�����AD=BC=8������������Ϊ8����2t��10��=18��2t���������Ϊ![]() .
.
����������S��t�ĺ�����ϵʽΪ .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�ı�AB��ADΪ�ױ߷ֱ�������������ABE�͵���������ADF.
��1�����ı���ABCDΪ������ʱ����ͼ�٣����Ա�AB��ADΪб�߷ֱ������������ֱ����ABE�͵���ֱ����ADF������BF��ED���߶�BF��ED��������ϵ��_____________��
��2�����ı���ABCDΪ����ʱ����ͼ�ڣ����Ա�AB��ADΪб�߷ֱ�������ڲࡢ���������ֱ����ABE�͵���ֱ����ADF������EF��BD���߶�EF��BD����������������ϵ����˵�����ɣ�
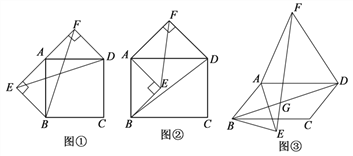
��3�����ı���ABCDΪƽ���ı���ʱ���Ա�AB��ADΪ�ױ߷ֱ���ƽ���ı����ڲࡢ�����������ABE�͵�����ADF������ABE����ADF�Ķ��Ǿ�Ϊ![]() ������EF��BD������ΪG.����
������EF��BD������ΪG.����![]() ��ʾ����FGD����˵������.
��ʾ����FGD����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���㳡�������λ�̳ABCD���ܳ���32�ף���A��60������A��C����֮��ľ���Ϊ�� ��

A. 4�� B. ![]() �� C. 8�� D.
�� C. 8�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����BAC=90�㣬��D������BC�ϣ���B��C���㲻�غϣ�����ADΪ����������ADEF��ʹ��E���B��ֱ��AD����࣬����BA������CF�ཻ�ڵ�G��
��1������D���߶�BC�ϣ���ͼ1��
�������ⲹȫͼ1��
���ж�BC��CG��������ϵ��λ�ù�ϵ��������֤����
��2������D���߶�BC���ӳ����ϣ���GΪCF�е㣬����GE��AB=![]() ����GE�ij�Ϊ_____����������GE����˼·��
����GE�ij�Ϊ_____����������GE����˼·��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�Ǿ���
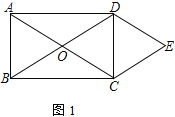

(1) ��ͼ1���Խ���AC��BD�ཻ�ڵ�O����DE��AC��CE��BD����֤���ı���OCED������
(2) ��ͼ2���Խ���AC��BD�ཻ�ڵ�O����BAD��ƽ���߽�BC�ڵ�F���ҡ�CAF��15������AF��FC��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������������ӡ�ʯͷ�����ӡ�������Ϸ�������ڲ����Ĵ����з�����״����С����ͬ��15�ſ�Ƭ������д��������������ʯͷ���������������������Ŀ�Ƭ�����ֱ�Ϊ2��3��4��6�����˸��������һ�ſ�Ƭ�������߲��Żأ�����ʤ������Լ������������ʤ��ʯͷ����������������ʯͷ��ʤ������������������ʤ��������������ʤ������������ʯͷ����ͬ�ֿ�Ƭ����ʤ����
��1����������������������ʯͷ���ĸ����Ƕ��٣�
��2����������������ʯͷ�������һ�ʤ�ĸ����Ƕ��٣�
��3�������������������������ֿ�Ƭ��ʤ�Ŀ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�˵�ƽ������3+2![]() ����1+
����1+![]() ��2������˼����С������������̽����
��2������˼����С������������̽����
����a+b![]() ����m+n
����m+n![]() ��2��m2+2n2+2mn
��2��m2+2n2+2mn![]() ������a��b��m��n����������
������a��b��m��n����������
����a��m2+2n2��b��2mn��
����С�����ҵ���һ�ְ�����a+b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
��1����a+b![]() ����m+n
����m+n![]() ��2����a��b��m��n��Ϊ����ʱ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a���� ����b���� ����
��2����a��b��m��n��Ϊ����ʱ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a���� ����b���� ����
��2����a+6![]() ����m+n
����m+n![]() ��2����a��m��n��Ϊ����������a��ֵ��
��2����a��m��n��Ϊ����������a��ֵ��
��3������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������н�����ͼ��ʾ��ƽ��ֱ������ϵxOy.��ABC���������㶼�ڸ���ϣ���A�������ǣ�4��4���������������⣺
��1������ABC����ƽ��5����λ���ȣ�����ƽ�ƺ��A1B1C1����д����A�Ķ�Ӧ��A1�����ꣻ
��2��������A1B1C1����y��ԳƵ���A2B2C2��
��3������ABC�Ƶ�C��ʱ����ת90����������ת�����A3B3C.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ�������
A.ֱ����һ�㵽����ֱ�ߵĴ��߶Σ������㵽ֱ�ߵľ��룻
B.��֪�߶�![]() ��
��![]() �ᣬ����
�ᣬ����![]() ������Ϊ��-1��2�������
��������-1��2�������![]() ��������-1��-2����-1��6����
��������-1��-2����-1��6����
C.��![]() ��
��![]() ��Ϊ�෴������
��Ϊ�෴������![]() ��
��
D.��֪����![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯��
�Ľ⼯��![]() ����
����![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com