
 如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.分析 (1)由点A在原点的左侧,到原点的距离为26个单位长度,可知点A表示的数为-26,根据点B在点A的右侧,点A与点B的距离为16个单位长度,得出点B表示的数为-10,由点C表示的数与点B表示的数互为相反数,得到点C表示的数为10;
(2)根据列出=速度×时间,可得PA=1×t=t,由PC=AC-PA可得PC=36-t;
(3)①在点Q向点C运动过程中,设点Q运动x秒追上点P,根据点Q追上点P时,点Q运动的路程=点P运动的路程,列出方程,解方程即可;
②分两种情况:点Q从A点向点C运动时,又分点Q在点P的后面与点Q在点P的前面;点Q从C点返回到点A时,又分点Q在点P的后面与点Q在点P的前面.
解答 解:(1)∵点A在原点的左侧,到原点的距离为26个单位长度,
∴点A表示的数为-26,
∵点A与点B的距离为16个单位长度,且点B在点A的右侧,
∴点B表示的数为-26+16=-10,
∵点C表示的数与点B表示的数互为相反数,
∴点C表示的数为10,
故答案为:-26,-10,10;
(2)PA=1×t=t,
PC=AC-PA=36-t,
故答案为:t,36-t;
(3)①在点Q向点C运动过程中,设点Q运动x秒追上点P,根据题意得
3x=x+16,
解得x=8.
答:在点Q向点C运动过程中,能追上点P,点Q运动8秒追上;
②分两种情况:
(Ⅰ)点Q从A点向点C运动时,
如果点Q在点P的后面,那么1x+16-3x=2,解得x=7,此时点P表示的数是-3;
如果点Q在点P的前面,那么3x-(1x+16)=2,解得x=9,此时点P表示的数是-1;
(Ⅱ)点Q从C点返回到点A时,
如果点Q在点P的后面,那么3x+1x+16+2=2×36,解得x=$\frac{27}{2}$,此时点P表示的数是$\frac{7}{2}$;
如果点Q在点P的前面,那么3x+1x+16=2×36+2,解得x=$\frac{29}{2}$,此时点P表示的数是$\frac{9}{2}$.
答:在点Q开始运动后,P、Q两点之间的距离能为2个单位,此时点P表示的数分别是-3,-1,$\frac{7}{2}$,$\frac{9}{2}$.
点评 本题考查了一元一次方程的应用,数轴,列代数式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


科目:初中数学 来源: 题型:解答题
 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD 的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD 的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
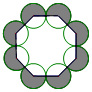 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
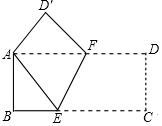 按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.
按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
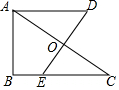 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com