
【题目】已知:把Rt△ABC和Rt△DEF按如图1摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm,如图2,△DEF从图1的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)用含t的代数式表示线段AP= ;
(2)当t为何值时,点E在∠A的平分线上?
(3)当t为何值时,点A在线段PQ的垂直平分线上?
(4)连接PE,当t=1(s)时,求四边形APEC的面积.

【答案】(1)(10﹣2t)cm.(2)![]() ;(3)t=2;(4)20
;(3)t=2;(4)20
【解析】
(1)利用勾股定理求出AB,根据AP=AB﹣BP计算即可.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.设TC=TH=x,证明Rt△ATH≌Rt△ATC(HL),推出AH=AC=8,在Rt△BTH中,则有(6﹣x)2=22+x2,求出x即可解决问题.
(3)根据线段垂直平分线的性质得到AP=AQ,根据等腰三角形的性质得到CE=CQ,根据勾股定理求出AB,列式计算即可.
(4)作PM⊥BE交BE于M,根据S四边形APEC=S△ABC﹣S△BPE计算算即可.
(1)在Rt△ABC中,∵∠ACB=90°,AC=8cm,BC=6cm,
∴AB=![]() =
=![]() =10(cm),
=10(cm),
由题意PA=AB﹣BP=(10﹣2t)cm,
故答案为(10﹣2t)cm.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.
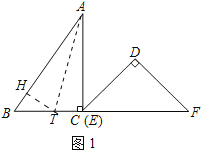
∵TC⊥AC,TH⊥AB,TA平分∠ABC,
∴TC=TH,∠AHT=∠ACT=90°,设TC=TH=x,
∵AT=AT,
∴Rt△ATH≌Rt△ATC(HL),
∴AH=AC=8,
∴BH=AB﹣AH=10﹣8=2,
在Rt△BTH中,则有(6﹣x)2=22+x2,
解得x=![]() ,
,
∴当t为![]() 时,点E在∠A的平分线上.
时,点E在∠A的平分线上.
(3)∵点A在线段PQ的垂直平分线上,
∴AP=AQ,
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°,
∴∠DEF=∠EQC,
∴CE=CQ,
由题意知:CE=t,BP=2t,
∴CQ=t,
∴AQ=8﹣t,
在Rt△ABC中,由勾股定理得,AB=10cm,
则AP=10﹣2t,
∴10﹣2t=8﹣t,
解得:t=2,
答:当t=2s时,点A在线段PQ的垂直平分线上;
(4)如图2中,过P作PM⊥BE,交BE于M,
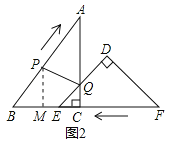
∴∠BMP=90°,
在Rt△ABC和Rt△BPM中,sinB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,PM=![]() ,
,
∵BC=6cm,CE=t,
∴BE=6﹣1=5,
∴S四边形APEC=S△ABC﹣S△BPE=![]() ×BC×AC﹣
×BC×AC﹣![]() ×BE×PM=
×BE×PM=![]() ×6×8﹣
×6×8﹣![]() ×5×
×5×![]() =20.
=20.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+6与y轴交于点B,直线l2:y=kx+6与x轴交于点A,且直线l1与直线l2相交所形成的角中,其中一个角的度数是75°,则线段AB的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
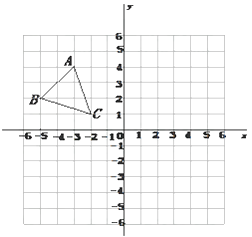
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为![]() 元/千克和
元/千克和![]() 元/千克(
元/千克(![]() 、
、![]() 都为正数,且
都为正数,且![]() ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
(1)用含![]() 、
、![]() 的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
(2)若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
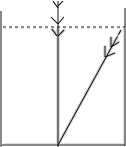
【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=![]() .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
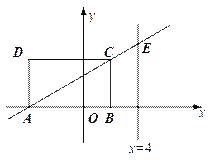
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com