
 ��1����������֤����
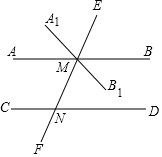
��1����������֤�������� ��1������M��ֱ��A1B1��ʹ��EMB1=��MND���������M ��������ֱ��AB��A1B1ƽ����ֱ��CD�����롰��ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�С�ì�ܣ����ɵó��𰸣�
��2������ƽ���ߵ����ʵó���EMB=��MND�����ɵó��𰸣�
���  ��1��֤��������EMB�١�MND������M��ֱ��A1B1��
��1��֤��������EMB�١�MND������M��ֱ��A1B1��
ʹ��EMB1=��MND��
��A1B1��CD��
�֡�AB��CD��
�����M ��������ֱ��AB��A1B1ƽ����ֱ��CD��
���롰��ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�С�ì�ܣ�
˵����EMA=��MND�Dz��Եģ�
������EMB=��MND��
�ʴ�Ϊ������ֱ��AB��A1B1ƽ����ֱ��CD����ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У���EMA=��MND����EMB=��MND��
��2����ͼ����ֱ֪��EF�ֱ�ֱ��AB��CD�ڵ�M��N��AB��CD��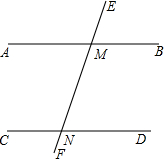
��֤����BMN+��MND=180�㣬
֤������AB��CD��
���EMB=��MND��
�ߡ�EMB+��BMN=180�㣬
���MND+��BMN=180�㣮
���� ���⿼����ƽ���ߵ����ʺ��ж�����������ö������������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
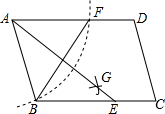 ��ͼ����?ABCD�У���ֱ�ߺ�Բ������BAD��ƽ����AG��BC�ڵ�E����BF=6��AB=4����AE�ij�Ϊ2$\sqrt{7}$��
��ͼ����?ABCD�У���ֱ�ߺ�Բ������BAD��ƽ����AG��BC�ڵ�E����BF=6��AB=4����AE�ij�Ϊ2$\sqrt{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ�˽����꼶ѧ���Ŀ�����ҵ�����ijѧУ�Ӹ��꼶ѧ���������ȡ��������ѧ���������ǵĿ�����ҵʱ�䣨��λ��min�����е��飬�����ռ��������������Ƴ�����������������ͼ���������ͼ����Ϣ������������⣺
Ϊ�˽����꼶ѧ���Ŀ�����ҵ�����ijѧУ�Ӹ��꼶ѧ���������ȡ��������ѧ���������ǵĿ�����ҵʱ�䣨��λ��min�����е��飬�����ռ��������������Ƴ�����������������ͼ���������ͼ����Ϣ������������⣺| ������ҵʱ�� �����飩 | ���� ��Ƶ���� |
| 30��45 | 5 |
| 45��60 | 12 |
| 60��75 | a |
| 75��90 | 10 |
| 90��105 | b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=x+b��ֱ��y=kx+6���ڵ�P��3��5���������x�IJ���ʽkx+6��x+b�Ľ⼯��x��3��
��ͼ��ֱ��y=x+b��ֱ��y=kx+6���ڵ�P��3��5���������x�IJ���ʽkx+6��x+b�Ľ⼯��x��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
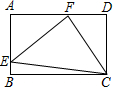 ��ͼ��E��F�ֱ��Ǿ���ABCD�ı�AB��AD�ϵĵ㣬��FEC=��FCE=45��
��ͼ��E��F�ֱ��Ǿ���ABCD�ı�AB��AD�ϵĵ㣬��FEC=��FCE=45���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
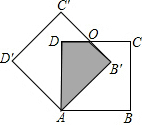 ��ͼ���߳�Ϊ1��������ABCD���Ƶ�A��ʱ����ת30��õ�������AB��C��D�䣬��ͼ����Ӱ���ֵ����Ϊ$\frac{{\sqrt{3}}}{3}$��
��ͼ���߳�Ϊ1��������ABCD���Ƶ�A��ʱ����ת30��õ�������AB��C��D�䣬��ͼ����Ӱ���ֵ����Ϊ$\frac{{\sqrt{3}}}{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com