
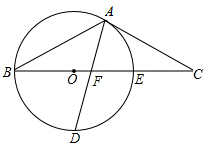
 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.分析 (1)连接OA,OD,如图,根据切线的性质得∠OAC=90°,即∠1+∠CAF=90°,根据垂径定理得到OD⊥BE,则∠D+∠2=90°,然后利用等量代换可得到∠3=∠CAF,于是根据等腰三角形的判定定理得到结论;
(2)在Rt△ODF中利用勾股定理计算.
解答 (1)证明:连接OA,OD,如图,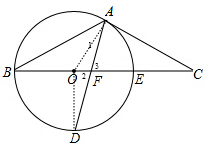 ∵AC是切线,
∵AC是切线,
∴OA⊥AC,
∴∠OAC=90°,即∠1+∠CAF=90°,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠D+∠2=90°,
∵∠1=∠D,∠2=∠3,
∴∠3=∠CAF,
∴AC=FC;
(2)解:在Rt△ODF中,OD=5,OF=2,
∴DF=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
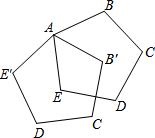 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
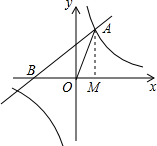 已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).
已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com