
 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ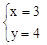 ”£
”£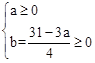 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ 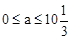 ”£
”£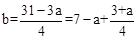 ĪŖÕūŹż£¬”ąa=1£¬5£¬9”£
ĪŖÕūŹż£¬”ąa=1£¬5£¬9”£


| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 µŲ³ö·¢Ļņ
µŲ³ö·¢Ļņ µŲŠŠ×ߣ¬Ķ¬Ź±ĻžŃō“Ó
µŲŠŠ×ߣ¬Ķ¬Ź±ĻžŃō“Ó µŲ³ö·¢Ļņ
µŲ³ö·¢Ļņ µŲŠŠ×ߣ¬ČēĶ¼ĖłŹ¾£¬Ļą½»ÓŚµćMµÄĮ½ĢõĻ߶Ī
µŲŠŠ×ߣ¬ČēĶ¼ĖłŹ¾£¬Ļą½»ÓŚµćMµÄĮ½ĢõĻ߶Ī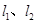 ·Ö±š±ķŹ¾Š”Ć÷”¢ĻžŃōĄėAµŲµÄ¾ąĄė
·Ö±š±ķŹ¾Š”Ć÷”¢ĻžŃōĄėAµŲµÄ¾ąĄė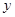 £ØĒ§Ć×£©ÓėŅŃÓĆŹ±¼ä
£ØĒ§Ć×£©ÓėŅŃÓĆŹ±¼ä £Ø·ÖÖÓ£©Ö®¼äµÄ¹ŲĻµ£¬
£Ø·ÖÖÓ£©Ö®¼äµÄ¹ŲĻµ£¬
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗĢīæÕĢā
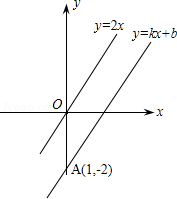
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗĢīæÕĢā
 x+bŗĶy£½
x+bŗĶy£½ xµÄĶ¼Ļó½»ÓŚµćP
xµÄĶ¼Ļó½»ÓŚµćP , Ōņøł¾ŻĶ¼ĻóæÉµĆ£¬¹ŲÓŚ
, Ōņøł¾ŻĶ¼ĻóæÉµĆ£¬¹ŲÓŚ  µÄ¶žŌŖŅ»“Ī·½³Ģ×éµÄ½āŹĒ____________£®
µÄ¶žŌŖŅ»“Ī·½³Ģ×éµÄ½āŹĒ____________£® 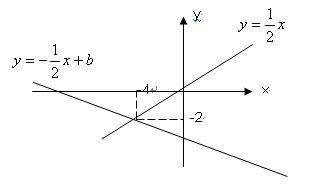
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
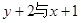 ³ÉÕż±ČĄż£¬µ±
³ÉÕż±ČĄż£¬µ±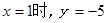
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā


 £ØĶņŌŖ£©ÓėĘäĻśŹŪĮæx£ØĶņŗŠ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Öø³öxµÄȔֵ·¶Ī§£»
£ØĶņŌŖ£©ÓėĘäĻśŹŪĮæx£ØĶņŗŠ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Öø³öxµÄȔֵ·¶Ī§£» £ØĶņŌŖ£©ÓėĀōøų²čŅ¶¾ĻśÉĢµÄĻśŹŪĮæx£ØĶņŗŠ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Öø³öxµÄȔֵ·¶Ī§£»
£ØĶņŌŖ£©ÓėĀōøų²čŅ¶¾ĻśÉĢµÄĻśŹŪĮæx£ØĶņŗŠ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Öø³öxµÄȔֵ·¶Ī§£»²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 )±¾”£
)±¾”£²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗĢīæÕĢā
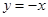 £¬Ö±Ļß
£¬Ö±Ļß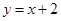 Óė
Óė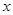 ÖįĪ§³ÉĶ¼ŠĪµÄÖܳ¤ŹĒ £Ø½į¹ū±£ĮōøłŗÅ£©£®
ÖįĪ§³ÉĶ¼ŠĪµÄÖܳ¤ŹĒ £Ø½į¹ū±£ĮōøłŗÅ£©£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com