
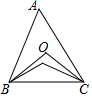
 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,可以得到∠BOC和∠BIC与∠A的关系,从而可以得到∠A的度数,进而求得sinA的值.
解答 解:∵O是△ABC的外心,
∴∠BOC=2∠A,
∵I是△ABC内切圆圆心,
∴∠BOC=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,
∵∠BOC=∠BIC,
∴2∠A=90°+$\frac{1}{2}$∠A,
解得,∠A=60°,
∴sinA=sin60°=$\frac{\sqrt{3}}{2}$,
故选D.
点评 本题考查三角形的内心和外心、解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
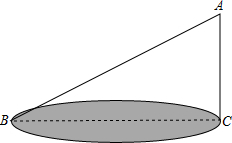 公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米)
公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,是一个几何体的俯视图和正视图(主视图),则该几何体的表面积为( )
如图所示,是一个几何体的俯视图和正视图(主视图),则该几何体的表面积为( )| A. | (5900+400π)cm2 | B. | (5900+500π)cm2 | C. | (1600+1650π)cm2 | D. | 7500cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
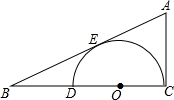 如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长.
如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
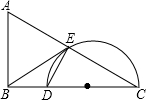 如图,在△ABC中,∠ABC=90°,AC的垂直平分线交BC于点D,交AC于点E.
如图,在△ABC中,∠ABC=90°,AC的垂直平分线交BC于点D,交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com