
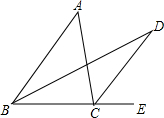
 如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?
如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律? 分析 根据角平分线的定义可得∠CBD=$\frac{1}{2}$∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCE,然后整理即可得到∠BDC=$\frac{1}{2}$∠A,代入数据计算即可得解.
解答 解:∵BD平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC,
∵CD平分△ABC的外角,
∴∠DCE=$\frac{1}{2}$∠ACE=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCD中,由三角形的外角性质,∠DCE=∠CBD+∠D=$\frac{1}{2}$∠ABC+∠D,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠BDC,
∴∠BDC=$\frac{1}{2}$∠A=$\frac{1}{2}$×50°=25°,
规律为:∠BDC=$\frac{1}{2}$∠A.
点评 本题考查了三角形的外角性质的应用,能正确运用性质进行推理和计算是解此题的关键,注意:三角形的一个外角等于和它不相邻的两个内角的和.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com