
【题目】潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为![]() 元,购买了
元,购买了![]() 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
(1)请求出![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围
的取值范围
(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
【答案】(1)![]() (
(![]() ,且
,且![]() 为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
【解析】
(1)根据题意“电子白板和台式电脑合共24台,一台电子白板每台9000元,一台台式电脑每台3000元”即可列出![]() 与
与![]() 的函数解析式,又根据“台式电脑的台数不超过电子白板台数的3倍”求出x的取值范围;
的函数解析式,又根据“台式电脑的台数不超过电子白板台数的3倍”求出x的取值范围;
(2)根据一次函数的性质即可得![]() 随
随![]() 的增大而增大,所以当
的增大而增大,所以当![]() 时,
时,![]() 有最小值.
有最小值.
解:(1)依题意可得:
![]()
![]() ,
,
∵台式电脑的台数不超过电子白板台数的3倍,
∴24-x≤3x
x≥6,
则x的取值范围为![]() ,且
,且![]() 为整数;
为整数;
(2)∵![]() ,
,![]() ,
,
∴![]() 随
随![]() 的增大而增大,∴当
的增大而增大,∴当![]() 时,
时,![]() 有最小值.
有最小值.
![]() (元)
(元)
答:当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象如图所示,以下结论:
的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
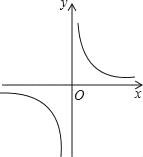
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
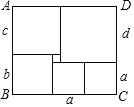
【题目】如图,长方形ABCD被分成六个小的正方,已知中间一个小正方形的边长为1,其它正方形的边长分别为a、b、c、d.观察图形并探索:(1)b=_____,d=_____;(用含a的代数式表示)(2)长方形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题(直接写出答案)
(1)2+(﹣2)= ;
(2)1﹣3= ;
(3)(﹣1)×(﹣3)= ;
(4)12÷(﹣3)= ;
(5)﹣32×![]() = ;
= ;
(6)(﹣4)2018×(﹣0.25)2019= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
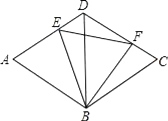
【题目】如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
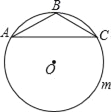
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
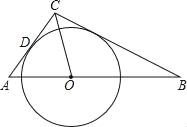
【题目】如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D.
(1)求证:⊙O与BC相切;
(2)当AC=3,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
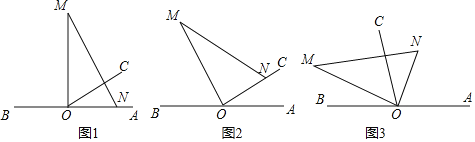
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com