
 如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内,再画第三条直线l3,那么这三条直线最多可有
如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内,再画第三条直线l3,那么这三条直线最多可有科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如图(1)所示,在等腰梯形ABCD中,AD∥BC,AB=CD,有两条动直线l1和l2从A点出发,且l1∥l2∥CD,l1以1 cm/s的速度沿AD的方向从左向右匀速运动,若干秒后,l2以一定的速度也沿AD的方向向右匀速运动,且l1和l2同时与CD重合.设l1,l2与梯形的边围成的图形周长为y cm,面积为S cm2,l1运动的时间为t s,如图(2)所示的是y与t之间的函数关系的图象,结合图象回答下列问题.
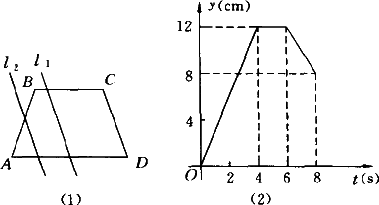
(1)求l2的速度;
(2)求梯形ABCD的面积;
(3)求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2003年台湾省中考数学试卷(解析版) 题型:选择题
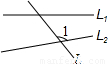
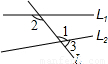
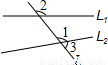
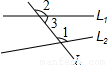

查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《相交线与平行线》(01)(解析版) 题型:选择题


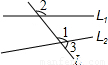
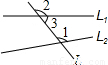
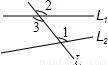
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com