Question

25、如图1，点G、F分别是等腰△ABC、等腰△ADE底边的中点，∠BAC=∠DAE=∠α，点P是线段CD的中点．试探索：∠GPF与∠α的关系，并加以证明．
说明：（1）如果你反复探索，没有解决问题，请写出探索过程（要求至少写3步）；
（2）在你完成（1）之后，可以从如图2，如图3中选取一个图，完成解答．

Answer 1

分析：∠GPF与∠α的关系是互为补角，
（1）连接BD，连接CE，由已知可证明△ABD≌△ACE，则∠ABD=∠ACE．因为G、P、F分别是BC、CD、DE的中点，则PG∥BD，PF∥CE．进而得出∠GPF=180°-∠α．
（2）选取图2或3都可以，例如图3，由AB=AC、AD=AE，得BD=CE，再根据G、P、F分别是BC、CD、DE的中点，可得出PG∥BD，PF∥CE．则∠GPF=180°-∠α．

解答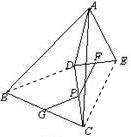：解：∠GPF=180°-∠α．
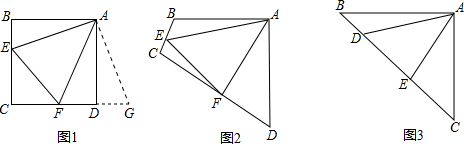
（1）证明：连接BD，连接CE．∵AB=AC、AD=AE，∠BAC=∠DAE
∴∠BAD=∠CAE∴△ABD≌△ACE，
∴∠ABD=∠ACE．∵G、P、F分别是BC、CD、DE的中点，
∴PG∥BD，PF∥CE．∴∠PGC=∠CBD，∠DPF=∠DCE=∠DCA+∠ACE=∠DCA+∠ABD，
∠DPG=∠PGC+∠BCD=∠CBD+∠BCD，
∠GPF=∠DPF+∠DPG=∠DCA+∠ABD+∠CBD+∠BCD=180°-∠BAC=180°-∠α，
即∠GPF=180°-∠α．
写探索过程要步步有据，写两步得（1分），写三步得（2分）．

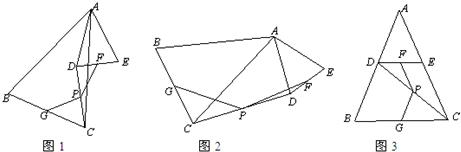
（2）选取图2证明：
连接BD，连接CE．
∵AB=AC、AD=AE，∠BAC=∠DAE，∴∠BAD=∠CAE，
∴△ABD≌△ACE，（5分）
∴∠ABD=∠ACE．
设BD与CE交于点O，AC与BD交于点K，∠AKB=∠CKO，
∴∠BOC=∠BAC，∠COD=180°-∠α．
∵G、P、F分别是BC、CD、DE的中点，
∴PG∥BD，PF∥CE．（8分）
∴∠GPC=∠BDC，∠DPF=∠DCE，（9分）
∠GPF=180°-∠GPC-∠DPF=180°-∠BDC-∠DCE=∠COD，
即∠GPF=180°-∠α．（10分）

选取图3证明：
∵AB=AC、AD=AE，∴BD=CE，（3分）
∵G、P、F分别是BC、CD、DE的中点，∴PG∥BD，PF∥CE．（4分）
∴∠ADC=∠DPG，∠DPF=∠ACD，∠GPF=∠DPF+∠DPG=∠ADC+∠ACD
=180°-∠BAC=180°-∠α，即∠GPF=180°-∠α．（5分）

点评：本题考查了全等三角形的判定和性质以及等腰三角形的性质，是一个变式训练题，难度偏大．