
分析 (1)根据已知规律写出④即可.
(2)根据已知规律写出n个等式,利用提公因式法即可证明规律的正确性.
(3)写出前101个等式,将这些等式相加,整理即可得出答案.
解答 解:(1)根据已知等式:
①21-20=2-1=20;
②22-21=4-2=21;
③23-22=8-4=22;
得出以下:
④24-23=16-8=23,
故答案为:24-23=16-8=23.
(2)①21-20=2-1=20;
②22-21=4-2=21;
③23-22=8-4=22;
④24-23=16-8=23;
得出第n个等式:
2n-2(n-1)=2(n-1);
证明:
2n-2(n-1),
=2(n-1)×(2-1),
=2(n-1);
故答案为:2n-2(n-1)=2(n-1);
(3)根据规律:
21-20=2-1=20;
22-21=4-2=21;
23-22=8-4=22;
24-23=16-8=23;
…
2101-2100=2100;
将这些等式相加得:
20+21+22+23+…+2100,
=2101-20,
=2101-1.
∴20+21+22+23+…+2100=2101-1.
点评 题目考查了数字的规律变化,解决此类问题的关键是找到序号和变化数字的关系,另外题目涉及证明和运算,对学生的考察能力有了更高的要求,题目整体艰难,适合课后培优训练.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{0.5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
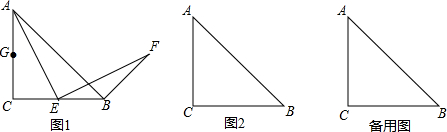
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com