
分析 (1)把$\frac{1}{\sqrt{n+1}+\sqrt{n}}$分母有理化即可;
(2)先利用分母有理化得到x=3-2$\sqrt{2}$,x=3+2$\sqrt{2}$,则易得x+y=6,x-y=-4$\sqrt{2}$,xy=1,然后把原式变形为2(x+y)(x-y)+7xy,再利用整体代入的方法计算.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1})^{2}-(\sqrt{n})^{2}}$=$\sqrt{n+1}$-$\sqrt{n}$;
故答案为$\sqrt{n+1}$-$\sqrt{n}$;
(2)∵x=($\sqrt{2}$-1)2=3-2$\sqrt{2}$,x=($\sqrt{2}$+1)2=3+2$\sqrt{2}$,
∴x+y=6,x-y=-4$\sqrt{2}$,xy=1,
∴原式=2(x+y)(x-y)+7xy
=2×6×(-4$\sqrt{2}$)+7×1
=7-48$\sqrt{2}$.
点评 本题考查了分母有理化:分母有理化是指把分母中的根号化去.分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
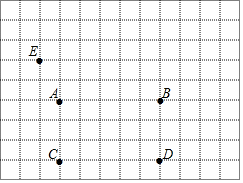 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com