
��ͼ��������AOCB��ƽ��ֱ������ϵ �У���OΪԭ�㣬��B�ڷ���������
�У���OΪԭ�㣬��B�ڷ��������� ��
�� ��
�� ��ͼ���ϣ���BOC�����Ϊ
��ͼ���ϣ���BOC�����Ϊ ��
��
��1���������� �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2��������E��A��ʼ��AB��B��ÿ��1����λ���ٶ��˶���ͬʱ����F ��B��ʼ��BC��C��ÿ�� ����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������
����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF������� ��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��3�����˶�ʱ��Ϊ ��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�⣺��1�����ı���AOCBΪ������ ����AB=BC=OC=OA��
���B������ ��
�� ����
����
�� ����
����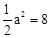 �����
�����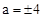 ��
��
�֡ߵ�B�ڵ�һ���ޣ����B����Ϊ��4��4����
����B��4��4������ ��
��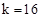 ��
��
�෴������������ʽΪ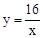 ��
��
��2�����˶�ʱ��Ϊt������E���ٶ�Ϊÿ��1����λ����F ���ٶ�Ϊÿ��2����λ��
��AE=t�� BF ��
��
��AB=4����BE=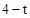 ��
��
�� ��
��
��S����t�ĺ�����ϵʽΪ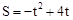 ����
���� ʱ����BEF��������
ʱ����BEF��������
��3�����ڡ�
��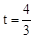 ʱ����E������Ϊ��
ʱ����E������Ϊ�� ��4������F������Ϊ��4��
��4������F��������4�� ����
����
����F����� ��ĶԳƵ�F1����F1��4��
��ĶԳƵ�F1����F1��4��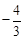 ����������E��F1��ֱ�ߣ�
����������E��F1��ֱ�ߣ�
��E ��4����F1��4��
��4����F1��4��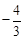 ���ɵ�ֱ��EF1�Ľ���ʽ��
���ɵ�ֱ��EF1�Ľ���ʽ�� ��
��
��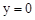 ʱ��
ʱ��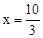 ����P�������Ϊ��
����P��������� ��0����
��0����
����E����� ��ĶԳƵ�E1����E1��
��ĶԳƵ�E1����E1��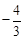 ��4����������E1��F��ֱ�ߣ�
��4����������E1��F��ֱ�ߣ�
��E1��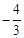 ��4����F��4��
��4����F��4�� ���ɵ�ֱ��E1F�Ľ���ʽ��
���ɵ�ֱ��E1F�Ľ���ʽ��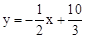 ��
��
�� ʱ��
ʱ��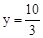 ����P�������Ϊ��0��
����P���������0�� ����
����
����������P�������ֱ�Ϊ�� ��0����0��
��0����0�� ����
����
���������������1�����������ε����ʺ͡�BOC�����Ϊ ����ʽ�����B�����꣬����
����ʽ�����B�����꣬���� ���������k���Ӷ���÷����������Ĺ�ϵʽ��
���������k���Ӷ���÷����������Ĺ�ϵʽ��
��2������˫������˶�ʱ����ٶȱ�ʾ��BF��BE���������S����t�ĺ�����ϵʽ����Ϊ����ʽ���ɸ��ݶ��κ�������ֵԭ����á�BEF��������ʱt��ֵ��
��3��������ԳƵ�ԭ������F����� ��ĶԳƵ�F1��E�����
��ĶԳƵ�F1��E����� ��ĶԳƵ�E1����������ۡ�
��ĶԳƵ�E1����������ۡ�


 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�׳�����·��ɲ�����飬�ռ������������±���ʾ��
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������ ��ֱ��
��ֱ�� ���ڵ�O��0��0����
���ڵ�O��0��0���� ����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
��1���������ߵĺ�������ʽ��
��2������CΪOA���е㣬��BC�ij���
��3����BC��BEΪ�߹�������BCDE�����D������Ϊ����������������֮��Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����������x�ύ��A��1��0����B����3��0�����㣬��y�ύ�ڵ�C��0��3�����������ߵĶ���ΪD��
��1����������ߵĽ���ʽ�붥��D�����꣮
��2�����жϡ�BCD����״����˵�����ɣ�
��3��̽�����������Ƿ���ڵ�P��ʹ����P��A��CΪ��������������BCD���ƣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������������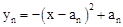 ��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1��������
��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1�������� ��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��1����a1,b1��ֵ��������y2�Ľ���ʽ��
��2��������y3�Ķ�������Ϊ�� �� ����
�������Ƶ�n��������yn�Ķ�������Ϊ�� �� ��;
���������ߵĶ�����������ĺ�����ϵ�� ��
��3��̽�����н��ۣ�
������An-1An��ʾ��n�������߱�x��صõ��߶γ���ֱ��д��A0A1��ֵ�������An-1An��
���Ƿ���ھ�����A��2��0����ֱ�ߺ����������߶��ཻ���ұ�ÿһ�������߽صõ��߶εij��ȶ���ȣ������ڣ�ֱ��д��ֱ�ߵı���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�����Ϊ��3��4���������߽� y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A������Ϊ��0����5����
��1����������ߵĽ���ʽ��
��2������B���߶�AB�Ĵ��߽����������D������Ե�CΪԲ�ĵ�Բ��ֱ��BD���У����ж������ߵĶԳ������C��λ�ù�ϵ��������֤����
��3�������������Ƿ����һ��P��ʹ��ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У������� �Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
��1����m=2ʱ�����B�����ꣻ
��2����DE�ij���
��3�������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���ڹ���D��AB��ƽ���ߣ���ڣ�3������ȷ���ĺ���ͼ�����һ������ΪP����mΪ��ֵʱ���ԣ�A��B��D��PΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����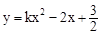 ��
�� �dz�����
�dz�����
��1�����ú�����ͼ���� ��ֻ��һ�����㣬��
��ֻ��һ�����㣬�� ��ֵ��
��ֵ��
��2������ ��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���
��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���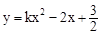 ����
���� ��
�� �������������
������������� Ӧ����������Լ�
Ӧ����������Լ� ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����������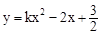 ��
�� �ύ��
�ύ�� ���㣬��
���㣬�� ��
�� ����
���� ���ϣ��Ƿ���ڵ�P��ʹ��ABP��ֱ�������Σ������ڣ������P����ABP��������������ڣ���˵�����ɡ�
���ϣ��Ƿ���ڵ�P��ʹ��ABP��ֱ�������Σ������ڣ������P����ABP��������������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
������y=��x2ƽ�ƺ��λ����ͼ��ʾ����A��B����ֱ�Ϊ����1��0������3��0������ƽ�ƺ����������y�ύ�ڵ�C���䶥��ΪD��
��1����ƽ�ƺ�������ߵĽ���ʽ�͵�D�����ꣻ
��2����ACB�͡�ABD�Ƿ���ȣ���֤����Ľ��ۣ�
��3����P��ƽ�ƺ�������ߵĶԳ����ϣ��ҡ�CDP���ABC���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com