
 如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )
如图,在平面直角坐标系中,OA⊥OB,sin∠OAB=$\frac{1}{2}$,点A、B分别在反比例函数y1=$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,则k的值是( )| A. | -$\frac{2}{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 作AC⊥x轴,BD⊥x轴.易得△ACO∽△ODB,根据比例式求出BD,OD,可得出点B的坐标,代入y=$\frac{k}{x}$即可求出k的值.
解答 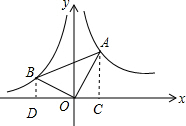 解:如图,作AC⊥x轴,BD⊥x轴.
解:如图,作AC⊥x轴,BD⊥x轴.
∵OA⊥OB,
∴∠AOB=90°,
∵∠OAC+∠AOC=90°,∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△ACO∽△ODB,
∴$\frac{OA}{OB}$=$\frac{OC}{BD}$=$\frac{AC}{OD}$,
∵sin∠OAB=$\frac{1}{2}$,
∴∠OAB=30°,
∴$\frac{OA}{OB}$=tan30°=$\sqrt{3}$,
设A(x,$\frac{2}{x}$)
BD=$\frac{\sqrt{3}}{3}$OC=$\frac{\sqrt{3}}{3}$x,OD=$\frac{\sqrt{3}}{3}$AC=$\frac{2\sqrt{3}}{3x}$,
∴B(-$\frac{2\sqrt{3}}{3x}$,$\frac{\sqrt{3}}{3}$x)
∴k=-$\frac{2\sqrt{3}}{3x}$×$\frac{\sqrt{3}x}{3}$=-$\frac{2}{3}$.
故选:A.
点评 本题主要考查了相似三角形的判定与性质及反比例函数图象上点的坐标特征,解题的关键是正确作出辅助线,构造相似三角形.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 银行存款500元,一年后可得利息171元 | |
| B. | 甲比乙重3kg,乙比甲小一岁 | |
| C. | 两班排球比赛,打满5局,甲班胜两局,乙班胜三局 | |
| D. | 两次测验,第一次得80分,第二次比第一次高6分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=2x-6,
已知一次函数y=2x-6,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
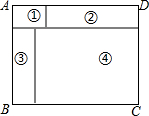 如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )
如图,矩形ABCD,由四块小矩形拼成(四块小矩形放置是既不重叠,也没有空隙),其中②③两块矩形全等,如果要求出①④两块矩形的周长之和,则只要知道( )| A. | 矩形ABCD的周长 | B. | 矩形②的周长 | C. | AB的长 | D. | BC的长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com