
| ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
| һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 | 7.6 | 8 | a | 3.82 | 70% | 30% |
| ���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 | b | 7.5 | 10 | 4.94 | 80% | 40% |
���� 1���ֱ���ƽ�����ļ��㹫ʽ�������Ķ����ɣ�
��2����ƽ�����ͷ�����⼴�ɣ�
��3���ɸ��ʹ�ʽ������������
��� �⣺��1����������8������4�Σ���࣬
������a=8��
b=$\frac{10��3+9+8+7+6��2+5+4}{10}$=7.5��
�ʴ�Ϊ��8��7.5��
��2�����һ���ƽ���ֱȶ���ߣ�����һ��ɼ��ȶ���ã�
��һ��ѧ���÷ֵķ���ȶ���С��˵��һ��ɼ��ȶ����ȶ���
��3��һ����5������ͬѧ��ÿ��ÿ�鵽�Ŀ�������ͬ������һ�����ֵ�ͬѧ��2λ��
�����ͬѧǡ����һ��ͬѧ�ĸ���Ϊ$\frac{1}{5}$��
���� ���⿼���˼�Ȩƽ��������������λ��������б�����״ͼ�����ʹ�ʽ������Ĺؼ����ܹ��б�����״ͼ�����еȿ��ܵĽ���оٳ������ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
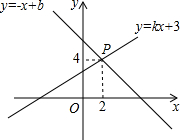 ��ͼ����֪һ�κ���y=kx+3��y=-x+b��ͼ���ڵ�P��2��4���������x�ķ���kx+3=-x+b�Ľ���x=2��
��ͼ����֪һ�κ���y=kx+3��y=-x+b��ͼ���ڵ�P��2��4���������x�ķ���kx+3=-x+b�Ľ���x=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
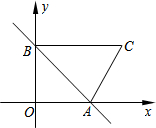 ��֪һ�κ���y=-x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��BC��x�ᣬ�ҡ�ACB������ֵΪ3��
��֪һ�κ���y=-x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��BC��x�ᣬ�ҡ�ACB������ֵΪ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
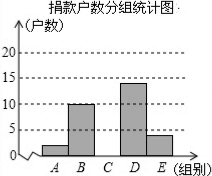 Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͼ����Ϣ����������
Ϊ���ø����ʧѧ��ͯ�ط�У��ij������֯���װ��������֡���������������־������е���ͷ���ͳ�ƺ�������������ͼ��ʾ��ͳ��ͼ��ͼ����Ϣ����������| ��� | ���x��Ԫ | ���� | Ƶ�� |
| A | 1��x��100 | 2 | 0.04 |
| B | 100��x��200 | 10 | 0.2 |
| C | 200��x��300 | 0.4 | |
| D | 300��x��400 | 14 | a |
| E | x��400 | 4 | 0.08 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
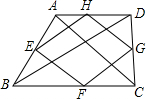 ��ͼ��˳�������ı���ABCD�����е�õ��ı���EFGH��Ҫʹ�ı���EFGHΪ���Σ�Ӧ���ӵ������ǣ�������
��ͼ��˳�������ı���ABCD�����е�õ��ı���EFGH��Ҫʹ�ı���EFGHΪ���Σ�Ӧ���ӵ������ǣ�������| A�� | AB��CD | B�� | AB=CD | C�� | AC��BD | D�� | AC=BD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com